# 力扣 hot100 题刷题

力扣 hot100 题刷题

🥇 代表复习过一遍，每道题最少复习三遍

牛客输入输出 JS 写法标准写法

// 单行输入 输入1,5  输出 6
//            2,6      8
while ((line = readline())) {
  var lines = line.split(" ");
  var a = parseInt(lines[0]);
  var b = parseInt(lines[1]);
  function add(m, n) {
    return m + n;
  }
  print(add(a, b));
}

// 多行输入
// 每调用一次 readline()就读取一行参数
/**
 * 输入 : 2       输出 6
 *        1  5        30
 *        10  20
 * */
var count = readline();
while ((line = readline())) {
  var lines = line.split(" ");
  var a = parseInt(lines[0]);
  var b = parseInt(lines[1]);
  // 每行输出
  print(a + b);
}

举例说明

https://www.jianshu.com/p/70a04abd0823

while ((line = readline())) {
  var lines = line.split(" ");
  var a = parseInt(lines[0]);
  var b = parseInt(lines[1]);
  print(a + b);
}

var count = readline();
while ((line = readline())) {
  var lines = line.split(" ");
  var a = parseInt(lines[0]);
  var b = parseInt(lines[1]);
  print(a + b);
}

while ((line = readline())) {
  var lines = line.split(" ");
  var a = parseInt(lines[0]);
  var b = parseInt(lines[1]);
  if (a === 0 && b === 0) break;
  print(a + b);
}

while ((line = readline())) {
  if (line == "0") break;
  let lines = line.split(" ");
  let sum = 0;
  for (let i = 0; i < lines[0]; i++) {
    sum += parseInt(lines[i + 1]);
  }
  print(sum);
}

var count = readline();
while ((line = readline())) {
  let sum = 0;
  let lines = line.split(" ");
  for (let i = 0; i < lines[0]; i++) {
    sum += parseInt(lines[i + 1]);
  }
  print(sum);
}

首先热身熟悉一下 dfs，bfs，先中后序遍历

// JS定义多维数组 mxn Array.from(arrayLike,mapFn)，第二个参数可选，新数组的每个元素都会执行这个回调
Array.from(Array(m), () => Array(n).fill(0));
// 深度优先 尽量深的遍历数，先访问根结点，再递归访问根结点的子结点
dfs = root => {
  console.log(root.val);
  root.children.forEach(dfs);
};

// 二叉树,携带层级 此时需要判断二叉树的左右子树情况
dfs = (root, level) => {
  if (!root) {
    return;
  }
  if (!root.left && !root.right && root.level) {
    console.log(root.val, level);
  }
  if (root.left) {
    dfs(root.left, level + 1);
  }
  if (root.right) {
    dfs(root.right, level + 1);
  }
};

// 广度优先，新建队列，对头出队，对头的children挨个入队
bfs = root => {
  let q = [root];
  while (q.length > 0) {
    const n = q.shift();
    console.log(n.val);
    n.children.forEach(item => {
      q.push(item);
    });
  }
};

// 二叉树的广度优先
bfs = (root, level) => {
  let q = [[root, 1]];
  while (q.length > 0) {
    const [n, level] = q.shift();
    if (n.left) {
      q.push([n.left, level + 1]);
    }
    if (n.right) {
      q.push([n.right, level + 1]);
    }
    if (!n.left && !n.right && level) {
      console.log(n.val);
    }
  }
};

// 先序遍历 非递归版 切记这里使用栈的数据结构

preOrder = root => {
  if (!root) {
    return;
  }
  let q = [root];
  while (q.length) {
    const n = q.pop();
    console.log(n.val);
    if (n.right) {
      q.push(n.right);
    }
    if (n.left) {
      q.push(n.left);
    }
  }
};

// 空栈 p指针指向root 左根右
inOrder = root => {
  if (!root) {
    return;
  }
  let q = [];
  let p = root;
  while (q.length || p) {
    while (p) {
      q.push(p);
      p = p.left;
    }
    const n = q.pop();
    console.log(n.val);
    // 指向右结点 遍历右结点去
    p = n.right;
  }
};

// 反向先序即可
postOrder = root => {
  if (!root) {
    return;
  }
  let q = [root];
  let outputStack = [];
  while (q.length) {
    const n = q.pop();
    outputStack.push(n);
    if (n.left) {
      q.push(n.left);
    }
    if (n.right) {
      q.push(n.right);
    }
  }
  return outputStack.reverse();
};

# 递归与回溯

计算递归的时间复杂度：https://zhuanlan.zhihu.com/p/129887381

一类题是排列组合题，一类是其他题

# 子集 (opens new window)(高频 ❤️❤️❤️)

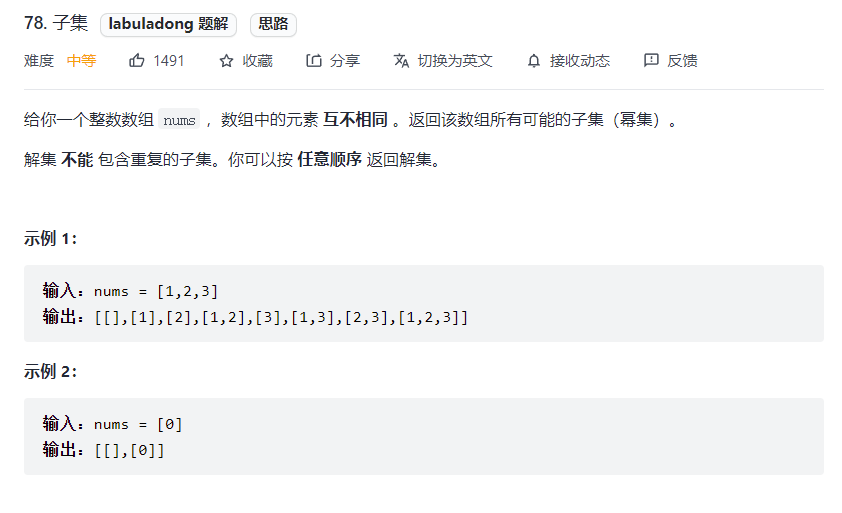
var subsets = function(nums) {
  /**
   * 排列组合题。求一个数组全子集,这道题同样也适用于求字符串的全子集
   * 回溯:
   * 路径: track，子集
   * 选择列表: nums
   * 结束条件: 满足子集数量小于等于集合数量
   */
  let res = [];
  let n = nums.length;
  // i代表子集元素数量
  function backTrack(track, i) {
    if (i <= n) {
      res.push(track);
    }
    // 保证子集数量在合法范围[i,n)
    for (let j = i; j < n; j++) {
      // 做选择
      track.push(nums[j]);
      // 递归,牢记浅拷贝一下
      backTrack(track.slice(), j + 1);
      // 撤销
      track.pop();
    }
  }
  backTrack([], 0);
  return res;
};

# 全排列 (opens new window)(高频 ❤️❤️❤️)

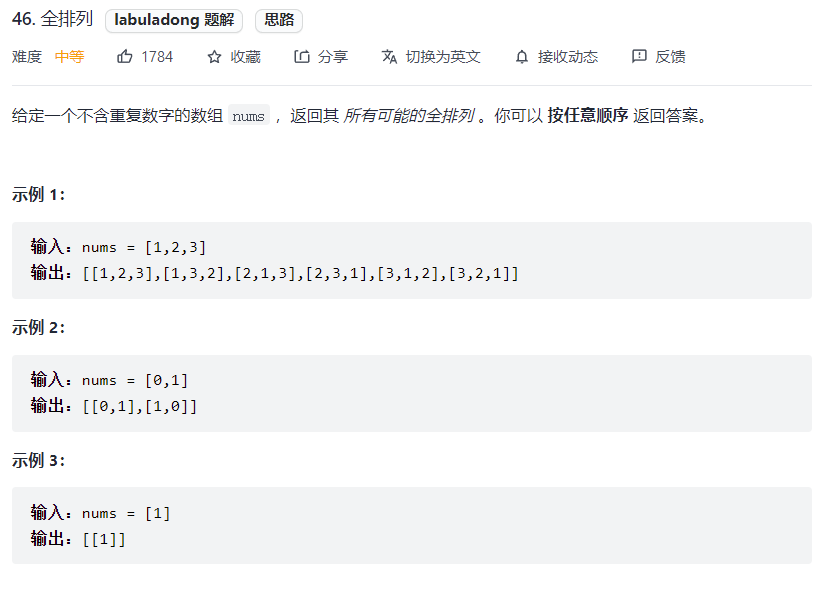
思路：使用回溯算法模板解题

// 1. 选择列表：[1,2,3]
// 2. 路径：track，每次允许重复
// 3. 结束条件: 到达策略树底部，路径元素和选择列表相同

function(nums){
  let res = []
  function backtrack(track){
    if(track.length === nums.length){
      res.push(track)
      return
    }
    for(let i=0;i<nums.length;i++){
      // 筛选条件，不允许路径理由重复的已选择结点
      if(track.includes(nums[i])){
        continue
      }
      // 选择操作
      track.push(nums[i])
      //递归
      backtrack(track.slice())
      //撤销
      track.pop()
    }

  }
  backtrack([])
  return res
}

# 组合总和 (opens new window)(高频 ❤️❤️❤️)

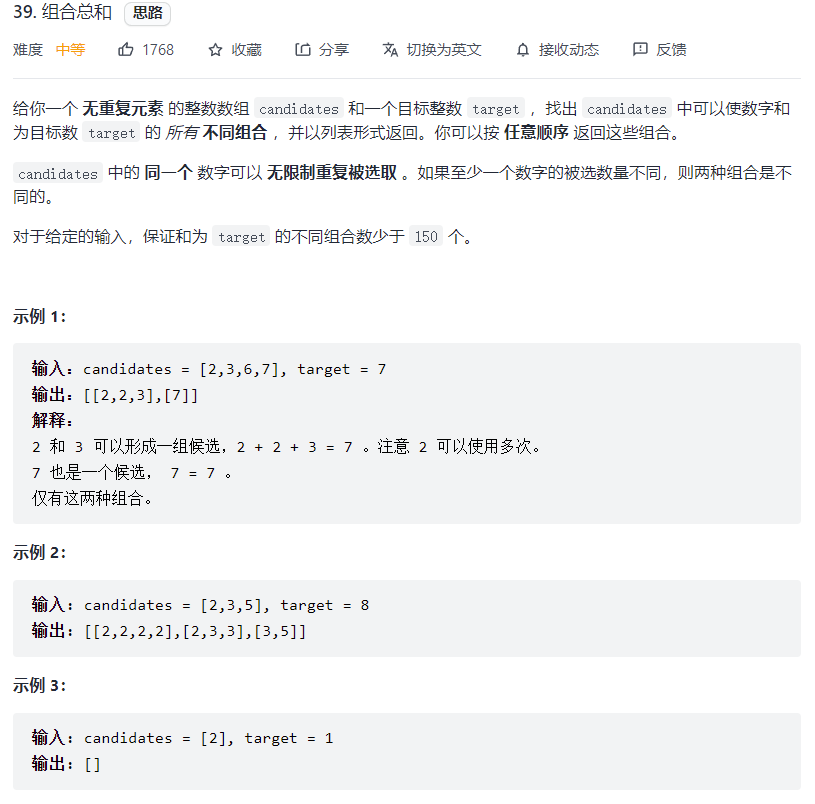
var combinationSum = function(candidates, target) {
  /**
   * 求目标和的组合
   * 回溯算法
   * 终止条件: rest === 0
   * 选择列表: candidates数组元素
   * track: 和为target的子集
   * 剪枝条件: rest < candidates[i] 永远都凑不齐，因为每个元素都大于剩余目标值
   */
  let res = [];
  let len = candidates.length;
  //这里排序是为了防止在for循环if判断时直接跳出了，比如这样的样例[8,7,4,3],11
  candidates.sort((x, y) => x - y);
  function backTrack(path, i, rest) {
    if (rest === 0) {
      res.push(path);
      return;
    }
    for (let j = i; j < len; j++) {
      //剪枝条件
      if (rest < candidates[j]) break;
      path.push(candidates[j]);
      backTrack(path.slice(), j, rest - candidates[j]);
      path.pop();
    }
  }
  backTrack([], 0, target);

  return res;
};

# 字母大小写全排列 (opens new window)

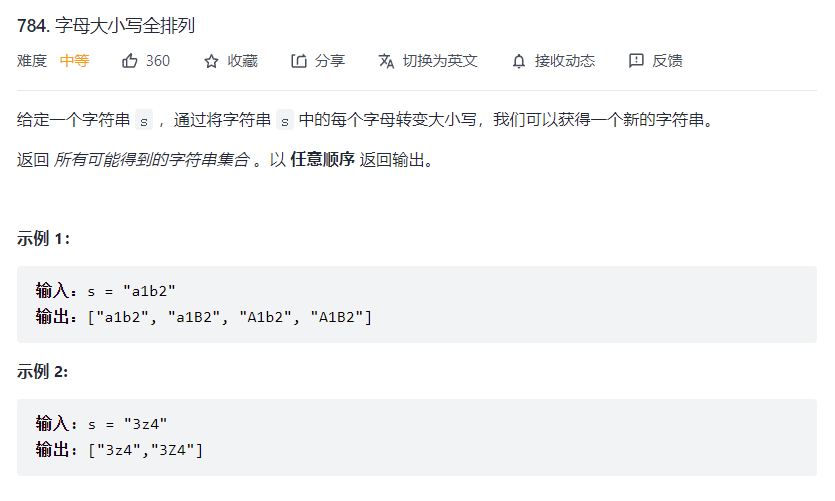
var letterCasePermutation = function(S) {
  /**
   * 回溯算法
   * 如果遍历到的是字母，则分别堆小写字母和大写字母进行回溯，如果是数字则进行拼接回溯
   * 选择条件: 是否是字母
   * 路径: 每次拼接的str
   * 结束条件: 当前遍历下标i === S.length,遍历完成
   */
  let res = [];
  let n = S.length;
  function backTrack(str, i) {
    if (i === n) {
      res.push(str);
      return;
    }
    let s = S[i];
    // 如果是字母，分别对大写或者小写进行回溯
    if ((s >= "a" && s <= "z") || (s >= "A" && s <= "Z")) {
      let lower = str + s.toLowerCase();
      let upper = str + s.toUpperCase();
      backTrack(lower, i + 1);
      backTrack(upper, i + 1);
    } else {
      backTrack(str + s, i + 1);
    }
  }
  backTrack("", 0);
  return res;
};

# 面试题 08.08. 有重复字符串的排列组合 (opens new window)

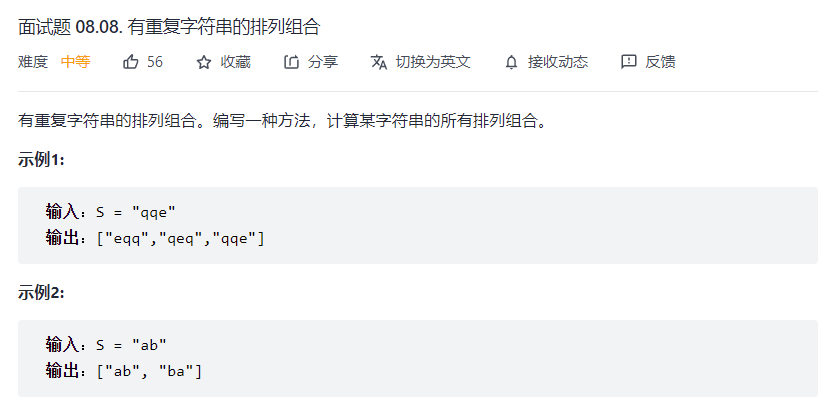
var permutation = function(S) {
  /**
   * 思路：对每个已选择的元素做标记,用visited记录，1代表选择，0代表未选择
   * 剪枝条件: S[i-1] === S[i] && visited[i-1] === 0
   * 选择列表:[0,S]
   * 路径:拼接好的字符串
   * */
  let n = S.length;
  let visited = new Array(n).fill(0);
  let res = [];
  S = S.split("")
    .sort()
    .join("");
  // str:拼接字符串
  function backTrack(str) {
    // 结束条件
    if (str.length === n) {
      res.push(str);
      return;
    }
    for (let i = 0; i < n; i++) {
      // 剪枝,如果当前字符已经被选择，或者当前字符和上一个字符(未被选择)重复，则剪枝
      if (visited[i] === 1) {
        continue;
      }
      if (S[i] === S[i - 1] && visited[i - 1] === 0) {
        continue;
      }
      visited[i] = 1;
      backTrack(str + S[i]);
      visited[i] = 0;
    }
  }

  backTrack("");
  return res;
};

# 全排列 II (opens new window)(高频 ❤️❤️❤️)

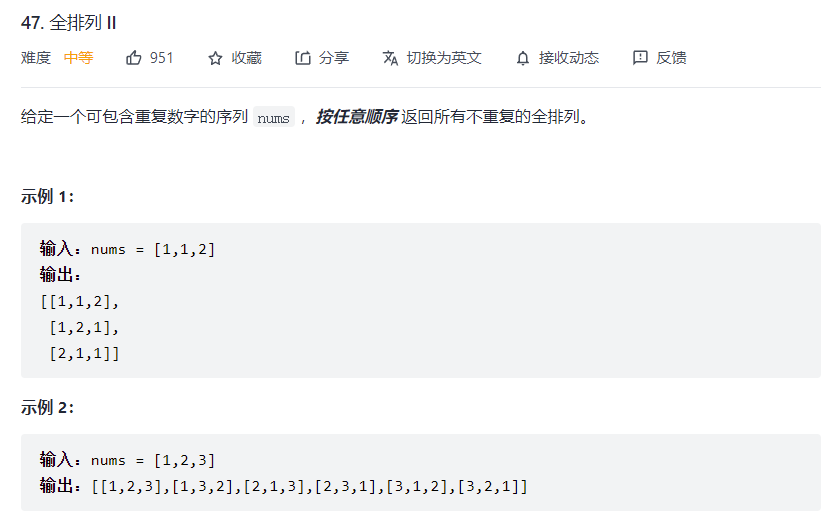
// 本题和全排列唯一区别是集合元素可重复,和上一道重复字符串排列逻辑相同，借助visited
var permuteUnique = function(nums) {
  let n = nums.length;
  let visited = new Array(n).fill(0);
  let res = [];
  // 排序
  nums.sort((a, b) => a - b);
  function backTrack(track) {
    if (track.length === n) {
      return res.push(track.slice());
    }
    for (let i = 0; i < n; i++) {
      if (visited[i] === 1) {
        continue;
      }
      if (visited[i - 1] === 0 && nums[i] === nums[i - 1] && i - 1 >= 0) {
        continue;
      }
      track.push(nums[i]);
      visited[i] = 1;
      brackTrack(track);
      track.pop();
      visited[i] = 0;
    }
  }
  brackTrack([]);
  return res;
};

# 分割回文串 (opens new window)

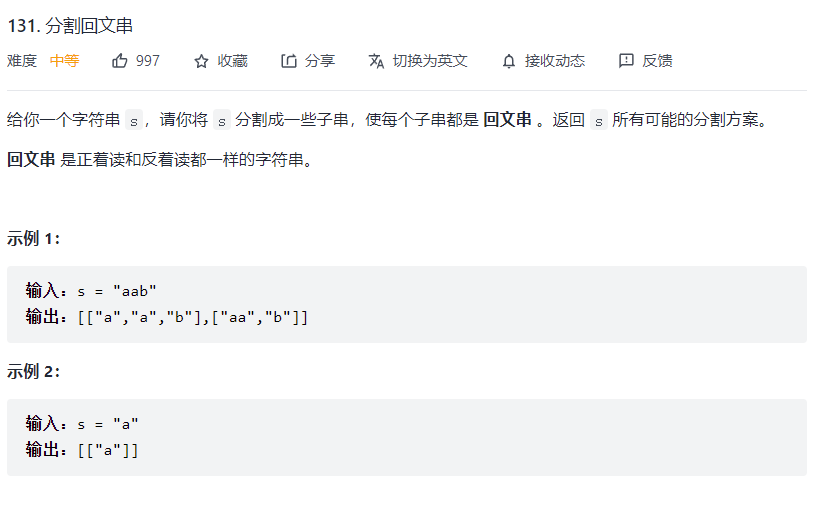
var partition = function(str) {
  // 关键点，截取的子串为 str[start,i+1]
  let res = [];
  // 判断回文
  function isPalindrome(s) {
    let head = 0;
    let tail = s.length - 1;
    while (head <= tail) {
      if (s[head] !== s[tail]) return false;
      head++;
      tail--;
    }
    return true;
  }
  // 如果start起始位置等于字符窜长度，则已经结束回溯
  function backtrack(path, start) {
    if (start === str.length) res.push(path);
    for (let i = start; i < str.length; i++) {
      // 取出截取的[start,i]子集，判断是否是回文子串
      console.log(i, str.slice(start, i + 1));
      if (!isPalindrome(str.slice(start, i + 1))) continue;
      path.push(str.slice(start, i + 1));
      backtrack(path.slice(), i + 1);
      path.pop();
    }
  }
  backtrack([], 0);
  return res;
};

# 复原 IP 地址 (opens new window)(高频 ❤️❤️❤️)

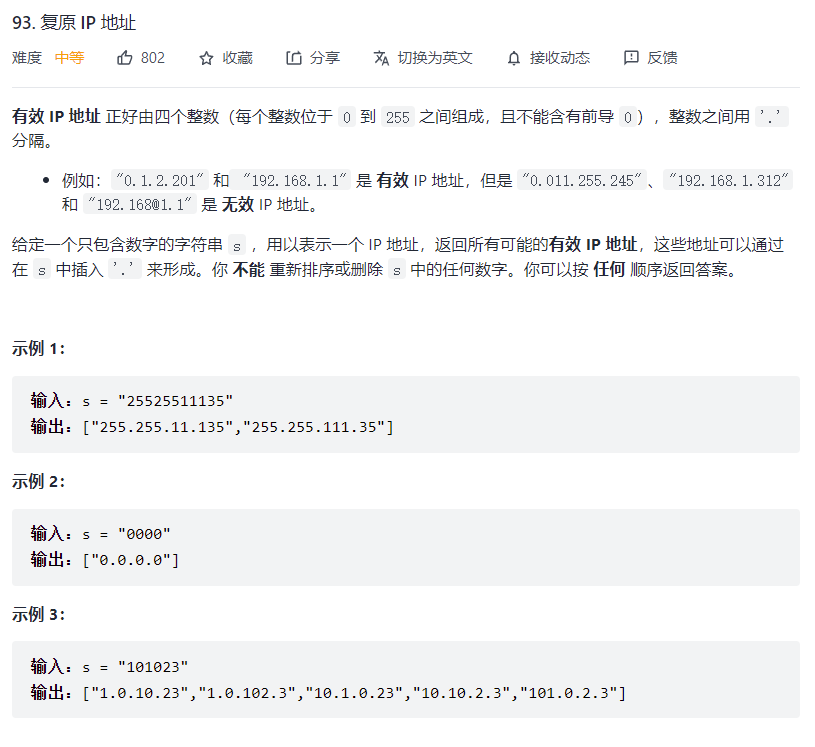
var restoreIpAddresses = function(s) {
  /**
   * 回溯算法
   * 用p表示段数，start表示当前遍历的下标,path为拼接的路径,如果s的长度小于4或者大于12，直接返回空数组
   *
   * 终止条件: 4段，并且当前的start === s.length，遍历完成
   * 选择列表: start下标到start+3的字符
   * track: 拼接的path
   * 剪枝条件: 每段的总和大于255，每段第一个字符等于‘0’
   */
  const len = s.length;
  if (len < 4 || len > 12) return [];
  const result = [];
  /**
   * start 当前遍历下标
   * p 当前段数
   * path 当前拼接字符串
   * */
  function backTrack(start, p, path) {
    if (p === 4) {
      if (start === len) result.push(path);
      return;
    }

    let c = "";
    for (let i = start; i < start + 3; i++) {
      c += s[i];
      if (s[start] === "0" || parseInt(c) > 255) break;
      // p === 3 代表下一段为最后一段，只不需要拼接 '.'
      backTrack(i + 1, p + 1, path + c + (p === 3 ? "" : "."));
    }
  }

  backTrack(0, 0, "");
  return result;
};

# 验证 IP 地址 (opens new window)(高频 ❤️❤️❤️)

var validIPAddress = function(IP) {
  const arr4 = IP.split(".");
  const arr6 = IP.split(":");
  if (arr4.length === 4) {
    //如果用正则表达式判断每组数小于256比较繁杂。这里先用正则判断是否为3位数字以内/^0$|^[1-9]\d{0,2}$/（注意单个0要单独判断，避免出现01.01.01.01这样的情况）
    if (arr4.every(part => part.match(/^0$|^([1-9]\d{0,2})$/) && part < 256)) {
      return "IPv4";
    }
  } else if (arr6.length === 8) {
    if (arr6.every(part => part.match(/^[0-9a-fA-F]{1,4}$/))) {
      return "IPv6";
    }
  }
  return "Neither";
};

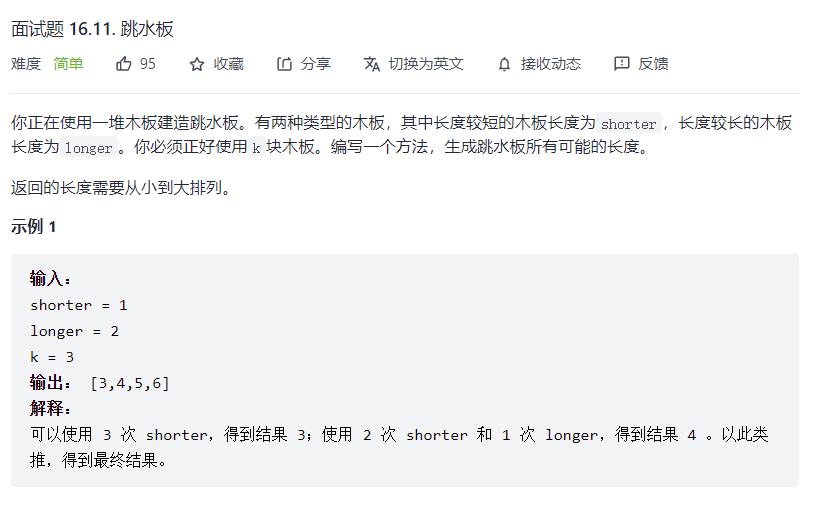
# 面试题 16.11. 跳水板 (opens new window)

var divingBoard = function(shorter, longer, k) {
  /**
   * 排列组合题，假设shorter数量为i，那么longer数量一定为k-i,而i的取值范围在[0,k]
   * 两种特殊情况:
   * k === 0
   * shorter === longer
   */
  if (k === 0) {
    return [];
  }
  if (shorter === longer) {
    return [k * shorter];
  }
  let res = [];
  for (let i = 0; i <= k; i++) {
    let longCount = i;
    let shortCount = k - i;
    res.push(shortCount * shorter + longCount * longer);
  }
  return res;
};

# 单词搜索 (opens new window)(高频 ❤️❤️❤️)

var exist = function(board, word) {
  /**
   * 回溯算法
   * 思路：首先找到首字母是否存在，然后保证上 右 下 左 四个方向进行搜索，如果不符合则返回上一个状态
   *
   * 结束条件: 当前遍历word的下标 i + 1 = word.length
   * 选择列表: 向上 向右 向左 向下
   * track： 当前word[i]
   */
  // 防止越界
  board[-1] = [];
  board.push([]);
  var m = board.length;
  var n = board[0].length;
  // 保证第一个字符和回溯顺利进行
  for (let row = 0; row < m; row++) {
    for (let col = 0; col < n; col++) {
      if (word[0] === board[row][col] && backTrack(row, col, 0)) {
        return true;
      }
    }
  }

  // 查找回溯
  function backTrack(y, x, i) {
    // 代表单词全部查找完毕
    if (i + 1 === word.length) {
      return true;
    }
    // 做选择
    let temp = board[y][x];
    board[y][x] = false;
    // 上右下左
    if (board[y - 1][x] === word[i + 1] && backTrack(y - 1, x, i + 1)) return true;
    if (board[y][x + 1] === word[i + 1] && backTrack(y, x + 1, i + 1)) return true;
    if (board[y + 1][x] === word[i + 1] && backTrack(y + 1, x, i + 1)) return true;
    if (board[y][x - 1] === word[i + 1] && backTrack(y, x - 1, i + 1)) return true;
    // 撤销选择
    board[y][x] = temp;
  }

  return false;
};

# N 皇后 (opens new window)

/**
 * @param {number} n
 * @return {string[][]}
 */
var solveNQueens = function(n) {
  /**
   * 1.选择列表：棋盘第row行的每一列都可以摆放皇后
   * 2. 路径：这里路径比较抽象，凡是小于row的行都已经摆放了皇后，row决定棋盘怎么摆放元素
   * 3. 结束条件；当row=棋盘最大行数N时
   */
  let res = [];
  function backstack(board, row) {
    if (row === n) {
      res.push(board);
      return;
    }
    for (let col = 0; col < n; col++) {
      //筛选不符合条件的结点
      if (!isValid(board, row, col)) {
        continue;
      }
      // 将决策树每一层拿出来
      const letter = board[row].split("");
      // 选择操作
      letter[col] = "Q";
      board[row] = letter.join("");
      // 递归 一定记得要做浅拷贝
      backstack(board.slice(), row + 1);
      // 撤销
      letter[col] = ".";
      board[row] = letter.join("");
    }
  }
  function isValid(xboard, row, col) {
    // 一列都不允许摆放 左上方和右上方都不允许摆放
    for (let i = 0; i < n; i++) {
      if (xboard[i][col] === "Q") {
        return false;
      }
    }
    // 左上方
    for (let i = row - 1, j = col - 1; i >= 0 && j >= 0; i--, j--) {
      if (xboard[i][j] === "Q") {
        return false;
      }
    }
    // 右上方
    for (let i = row - 1, j = col + 1; i >= 0 && j < n; i--, j++) {
      if (xboard[i][j] === "Q") {
        return false;
      }
    }
    return true;
  }
  // 初始化棋盘
  backstack(Array(n).fill(".".repeat(n)), 0);
  return res;
};

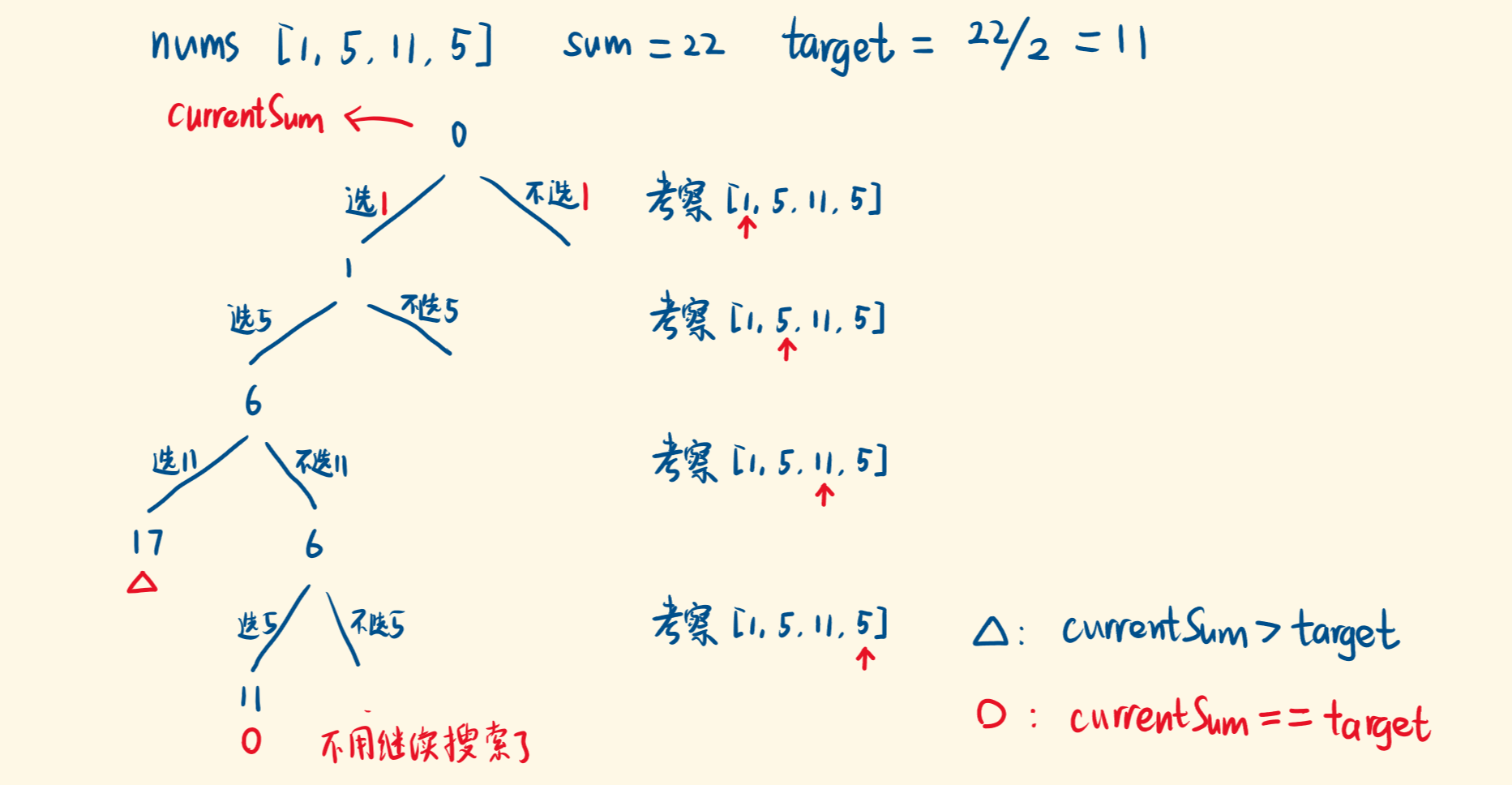
# 分割等和子集 (opens new window)

/**
 * @param {number[]} nums
 * @return {boolean}
 */
var canPartition = function(nums) {
  // 题意: 给你一个非空数组，和为sum，你能否找到一个子序列，和为sum/2
  let sum = 0;
  for (let num of nums) {
    sum += num;
  }
  // 非奇数
  if (sum % 2 !== 0) return false;
  const target = sum / 2;
  const memoMap = new Map();

  function backtrack(curSum, i) {
    // 超过，或者遍历完成
    if (curSum > target || i === nums.length) {
      return false;
    }
    if (curSum === target) {
      return true;
    }
    const key = curSum + "&" + i;
    // 备忘录
    if (memoMap.has(key)) {
      return memoMap.get(key);
    }
    // 选或者不选
    const res = backtrack(curSum + nums[i], i + 1) || backtrack(curSum, i + 1);
    memoMap.set(key, res);
    return res;
  }
  return backtrack(0, 0);
};

# 栈和队列

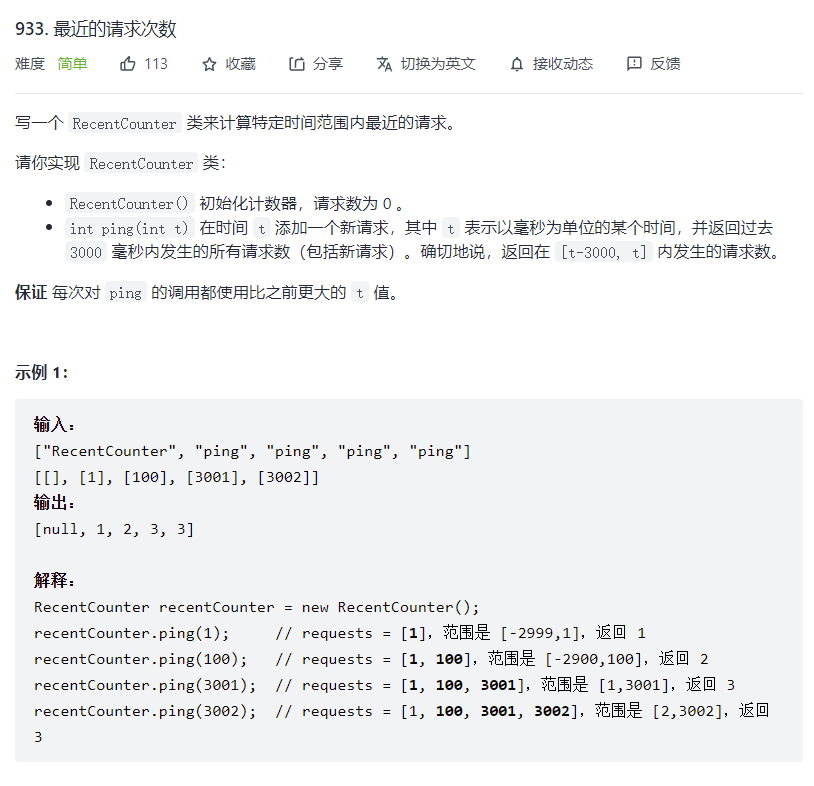
# 最近的请求次数 (opens new window)

RecentCounter.prototype.ping = function(t) {
  // q队列：保存请求事件在[t-3000,t]的请求时长 t 数组，如果q[0] < t-3000,也就是请求市场超出范围，就将这个队列出队，直到满足条件最后返回队列长度即可
  this.q.push(t);
  //
  while (this.q[0] < t - 3000) {
    this.q.shift();
  }
  return this.q.length;
};

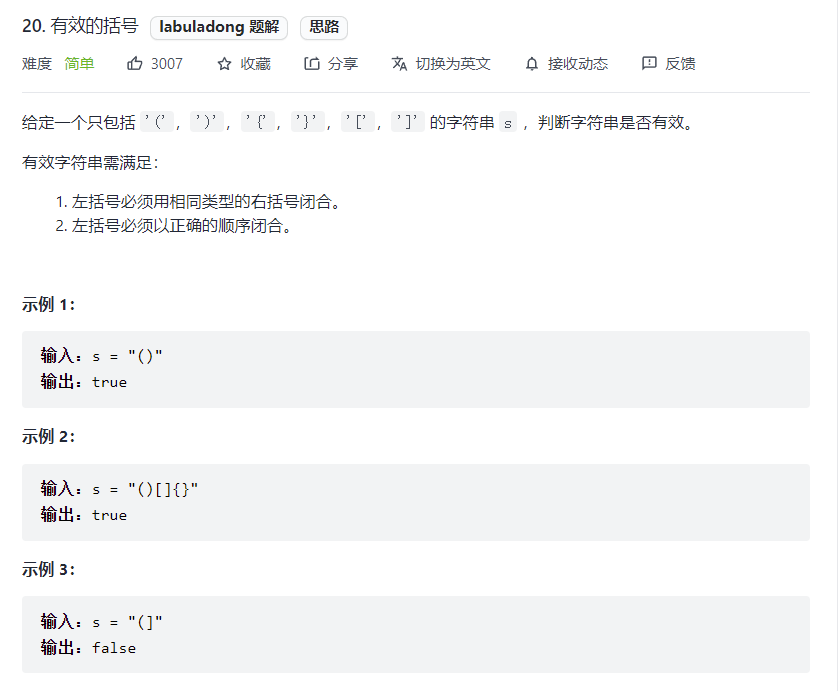
# 有效的括号 (opens new window)(高频 ❤️❤️❤️)

var isValid = function(s) {
  /**
   * 思路：遍历字符串，遇到左边的符号入栈，否则比较栈顶元素和当前遍历字符是否匹配完全，如果匹配完全就出栈，如果匹配失败返回false
   * 最后判断栈的长度是否是0即可
   * 特殊情况：栈长度为奇数直接返回false
   */
  let stack = [];
  if (s.length % 2 === 1) {
    return false;
  }
  for (let i = 0; i < s.length; i++) {
    let c = s[i];
    if (c === "(" || c === "[" || c === "{") {
      stack.push(c);
    } else {
      let p = stack[stack.length - 1];
      if ((p === "(" && c === ")") || (p === "[" && c === "]") || (p === "{" && c === "}")) {
        stack.pop();
      } else {
        return false;
      }
    }
  }
  return stack.length === 0;
};

# 计数二进制子串 (opens new window)

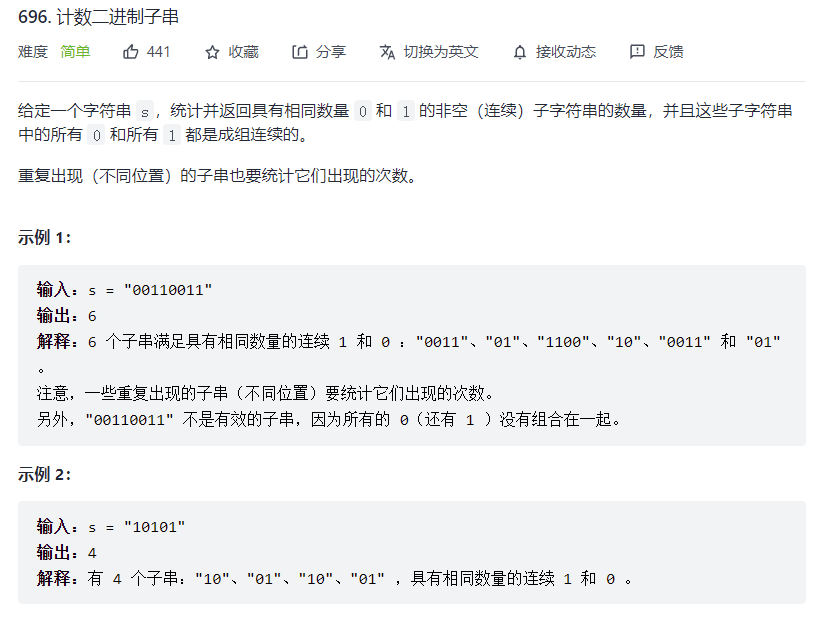
var countBinarySubstrings = function(s) {
  /**
   * 思路：借鉴官方,利用counts数组解决
   * 例如 [00110011],这里使用counts数组表示0,1个数分段数组 [2,2,2,2]
   * 然后counts数组相邻元素假设为u,v 可能存在u个1，v个0或者u个0，v个1。
   * 最后可以拿到的子串组合个树为min{u,v}，累加即可得到结果
   *
   */
  let counts = [];
  let ptr = 0;
  while (ptr < s.length) {
    const c = s.charAt(ptr);
    let count = 0;
    // 如果元素相同
    while (s.charAt(ptr) === c) {
      ++count;
      ++ptr;
    }
    counts.push(count);
  }
  let countNum = 0;
  for (let i = 1; i < counts.length; i++) {
    countNum += Math.min(counts[i - 1], counts[i]);
  }
  return countNum;
};

# 最小栈 (opens new window)(高频 ❤️❤️❤️)

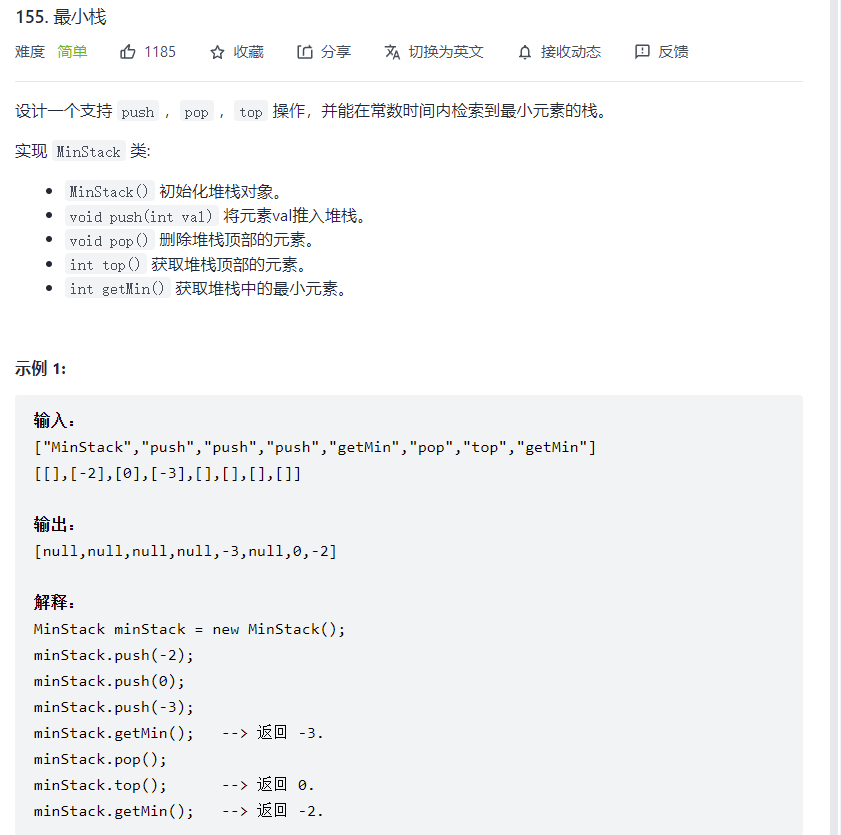
class MinStack {
  /**
   * 思路: 栈的每个元素都保存它前面所有元素的最小值
   */
  constructor() {
    this.stack = [];
  }
  get size() {
    return this.stack.length;
  }
  push(x) {
    // 每个stack元素多保存一个属性，前面所有元素的最小值
    this.stack.push({
      val: x,
      min: this.size ? Math.min(x, this.getMin()) : x
    });
  }
  pop() {
    this.stack.pop();
  }
  top() {
    return this.stack[this.size - 1].val;
  }
  getMin() {
    // 最小值就是栈顶元素的min属性
    return this.stack[this.size - 1].min;
  }
}

# 输出数组元素右侧第一个元素大于该元素的下标数组

// 找出每个数组元素右侧第一个比当前数大的数的下标，时间复杂度O(N)
// 例：输入[1, 3, 2, 5, 4, 6, 7, 10]，输出[1, 3, 3, 5, 5, 6, 7, -1]
const func = nums => {
  const stack = [[0, nums[0]]];
  const res = Array(nums.length).fill(-1);
  for (let i = 1; i < nums.length; i++) {
    // 如果栈顶小于nums[i] , res[i] = i,然后出栈
    while (stack.length && nums[i] > stack[stack.length - 1][1]) {
      res[stack[stack.length - 1][0]] = i;
      stack.pop();
    }
    stack.push([i, nums[i]]);
  }
  return res;
};

console.log(func([1, 3, 2, 5, 4, 6, 7, 10]));

# 用栈实现队列 (opens new window)(高频 ❤️❤️❤️)

/**
 * Initialize your data structure here.
 */

class MyQueue {
  /**
   * 上面两张图看完完全可以解释什么思路
   */
  constructor() {
    this.stack1 = []; // 原始栈
    this.stack2 = []; // 辅助栈 其实可以看成队列
  }
  push(x) {
    this.stack1.push(x);
  }
  pop() {
    // 栈1出栈 栈2入栈，然后栈2的栈顶就相当于对头 出栈即出队，最后还原栈1
    while (this.stack1.length) {
      this.stack2.push(this.stack1.pop());
    }
    let res = this.stack2.pop();
    while (this.stack2.length) {
      this.stack1.push(this.stack2.pop());
    }
    return res;
  }
  peek() {
    // 找到对头就是找到栈2的栈顶
    while (this.stack1.length) {
      this.stack2.push(this.stack1.pop());
    }
    let res = this.stack2[this.stack2.length - 1];
    while (this.stack2.length) {
      this.stack1.push(this.stack2.pop());
    }
    return res;
  }
  empty() {
    return !this.stack1.length;
  }
}

# 用队列实现栈 (opens new window)(高频 ❤️❤️❤️)

class MyStack {
  /**
   * 队列实现栈 出栈也就是相当于删掉队尾，这里需要借助中间队列，将原队列出队至一个元素也就是剩队尾，出队元素保存到中间队列，原队列出队即代表出队，最后恢复原队列
   */
  constructor() {
    this.queue = [];
  }
  push(x) {
    this.queue.push(x);
  }
  pop() {
    var queue1 = [];
    // 原队列只保留一个
    while (this.queue.length > 1) {
      queue1.push(this.queue.shift());
    }
    // 删除队尾 - 完成出栈
    let res = this.queue.shift();
    // 恢复原队列
    while (queue1.length) {
      this.queue.push(queue1.shift());
    }
    // 最后返回
    return res;
  }
  top() {
    // 栈顶就是队尾
    return this.queue[this.queue.length - 1];
  }
  empty() {
    return !this.queue.length;
  }
}

# 字符串解码 (opens new window)(高频 ❤️❤️❤️)

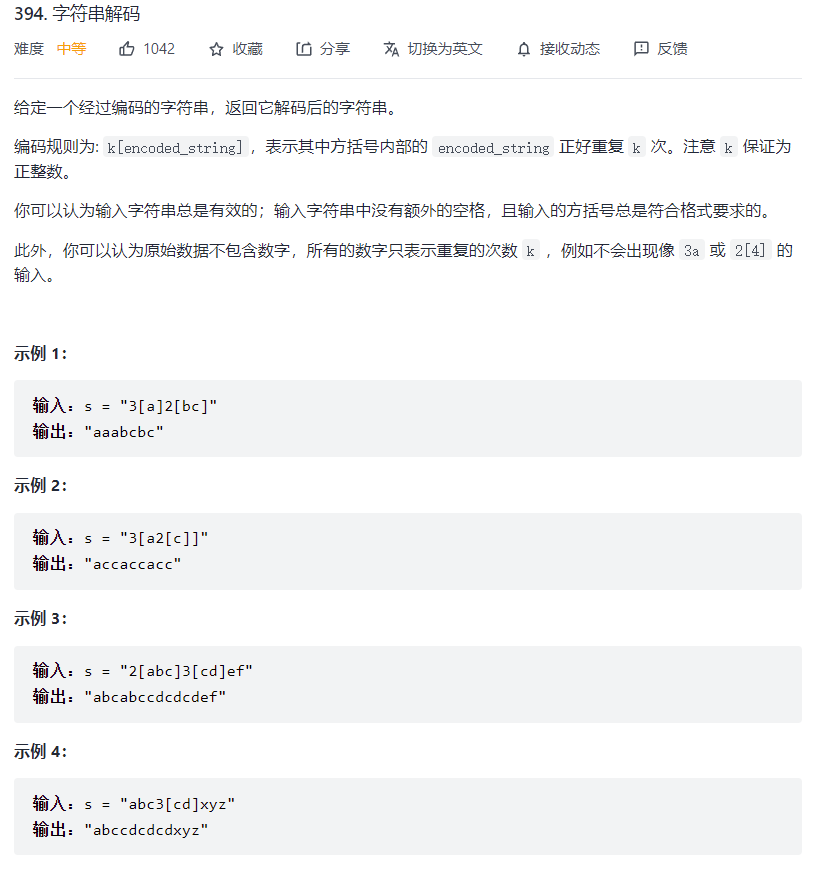
var decodeString = function(s) {
  /**
   * 思路：使用重复次数栈和累计字符栈进行维护，需要明确遇到四种类型的字符需要做些什么
   *
   * 1. 数字 因为可能是连续的,累计次数 = 累计次数*10 + (累计次数 - '0')
   * 2. 字符 resStr += cur
   * 3. [ 遇到左括号，就把当前的resStr和repeat入栈，然后置空这两个变量
   * 4. ] 遇到有括号，首先将重复次数栈的栈顶出栈，然后计算出重复的字符，最后和累计字符串栈顶连接，更新resStr
   */

  let repeatStack = []; // 重复次数栈
  let resStrStack = []; // 累计字符栈
  let resStr = ""; // 最后返回串
  let repeat = 0;
  for (let i = 0; i < s.length; i++) {
    let cur = s[i];
    if (cur === "[") {
      repeatStack.push(repeat);
      resStrStack.push(resStr);
      // 置空
      repeat = 0;
      resStr = "";
    } else if (cur === "]") {
      let temp = "";
      // 次数栈顶
      let num = repeatStack.pop();
      for (let i = 0; i < num; i++) {
        temp += resStr;
      }
      // 和累计字符串栈顶（上一个字符串）连接
      resStr = resStrStack.pop() + temp;
    } else if (cur >= "0" && cur <= "9") {
      repeat = repeat * 10 + (cur - "0");
    } else {
      resStr += cur;
    }
  }
  return resStr;
};

# 根据身高重建队列 (opens new window)

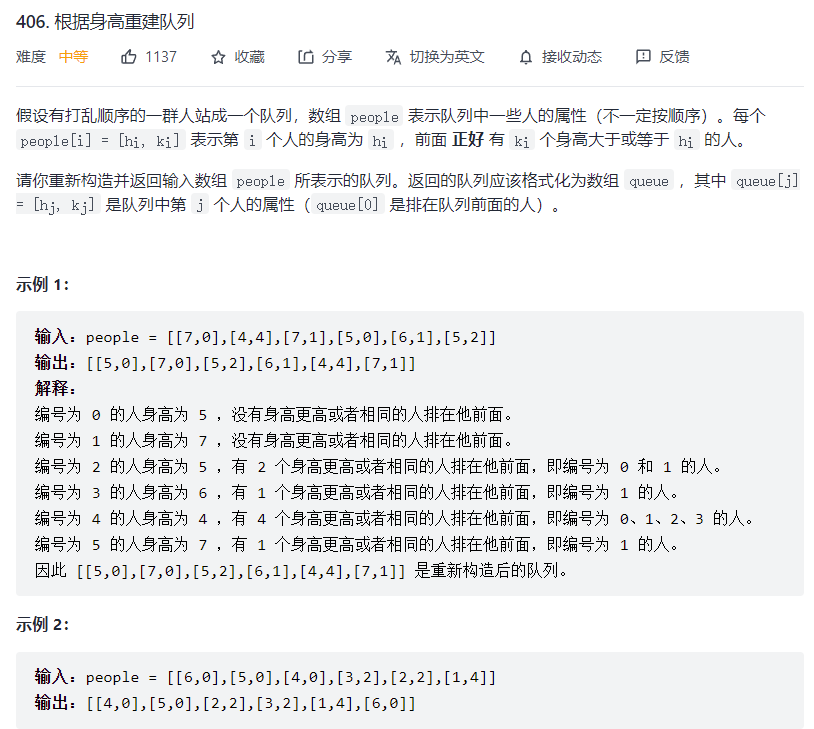
var reconstructQueue = function(people) {
  /**
   * 思路：
   * 1. 队列按照身高降序，身高相同的人人数多的排后面，人数少的排前面
   * 2. 排好序后的队列人数就是下标，将队列元素插到制定数组下标，返回即可
   */
  if (!people) {
    return;
  }
  // 首先降序排序好
  people = people.sort((a, b) => (a[0] === b[0] ? a[1] - b[1] : b[0] - a[0]));
  let res = [];
  for (let i = 0; i < people.length; i++) {
    // 插入的位置就是人数，有一个先后顺序插入的
    res.splice(people[i][1], 0, people[i]);
  }
  return res;
};

# 栈的压入、弹出序列 (opens new window)

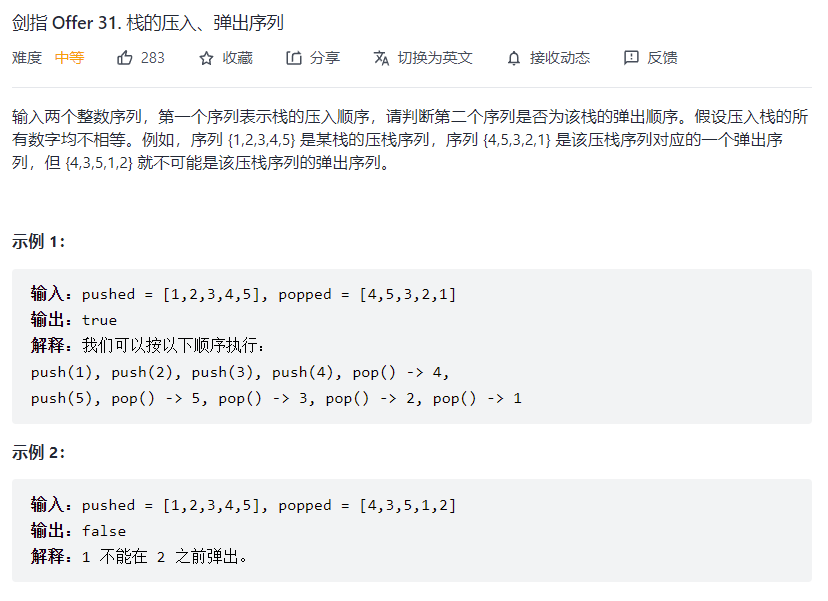
var validateStackSequences = function(pushed, popped) {
  /**
   * 思路： 设置一个辅助栈，如果辅助栈最后为空则满足条件，如果辅助栈栈顶和pop栈当前元素相同，出栈
   * !!! 注意这里使用unshift() 将push栈压入辅助栈 shift，出辅助栈元素
   * 案例： push [1,2,3,4] pop[4,3,2,1]
   * 1. stack = [4,3,2,1] k = 0 ,stack.length && popped[k]!==null && stack[0] === pop[k],stack.shift()
   * 2. stack = [3,2,1] k=1 stack[0] !==null && popped[k]!==null && stack[0] === pop[k]  ,satck.shift()
   * .....
   */
  let stack = [];
  let k = 0;
  // 辅助栈入栈
  for (let i = 0; i < pushed.length; i++) {
    stack.unshift(pushed[i]);
    // while循环 pop和stac栈顶存在，如果相等，出栈
    while (stack.length && popped[k] !== null && popped[k] === stack[0]) {
      stack.shift();
      k++;
    }
  }
  return stack.length === 0;
};

# 链表

# 反转链表 (opens new window)(高频 ❤️❤️❤️)

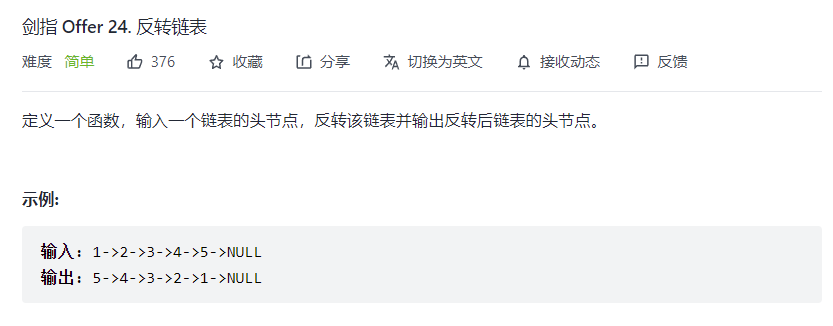
1>2>3>4>null => null>4>3>2>1

思路；要想把链表的箭头全部反向指，就要遍历头部和尾部，遍历过程互相赋值即可

var revirseListNode = head => {
  let p1 = head;
  let p2 = null;
  while (p1) {
    const temp = p1.next;
    // p1的下一个指针指向p2
    p1.next = p2;
    // 保证链表能走下去
    p2 = p1;
    p1 = temp;
  }
  return p2;
};

递归版

var reverseList = function(head) {
  /**
   * 递归版 cur :p1, pre:p2
   */
  let reverse = (pre, cur) => {
    if (!cur) {
      return pre;
    }
    // 保存p1.next
    let temp = cur.next;
    cur.next = pre;
    // 让递归去遍历链表去，传入的参数为p1,p1.next
    return reverse(cur, temp);
  };
  return reverse(null, head);
};

# 反转链表 II (opens new window)(高频 ❤️❤️❤️)

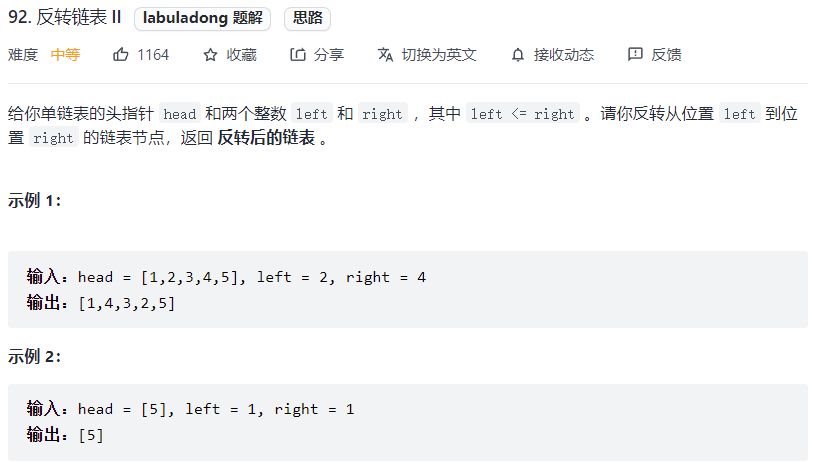
思路:

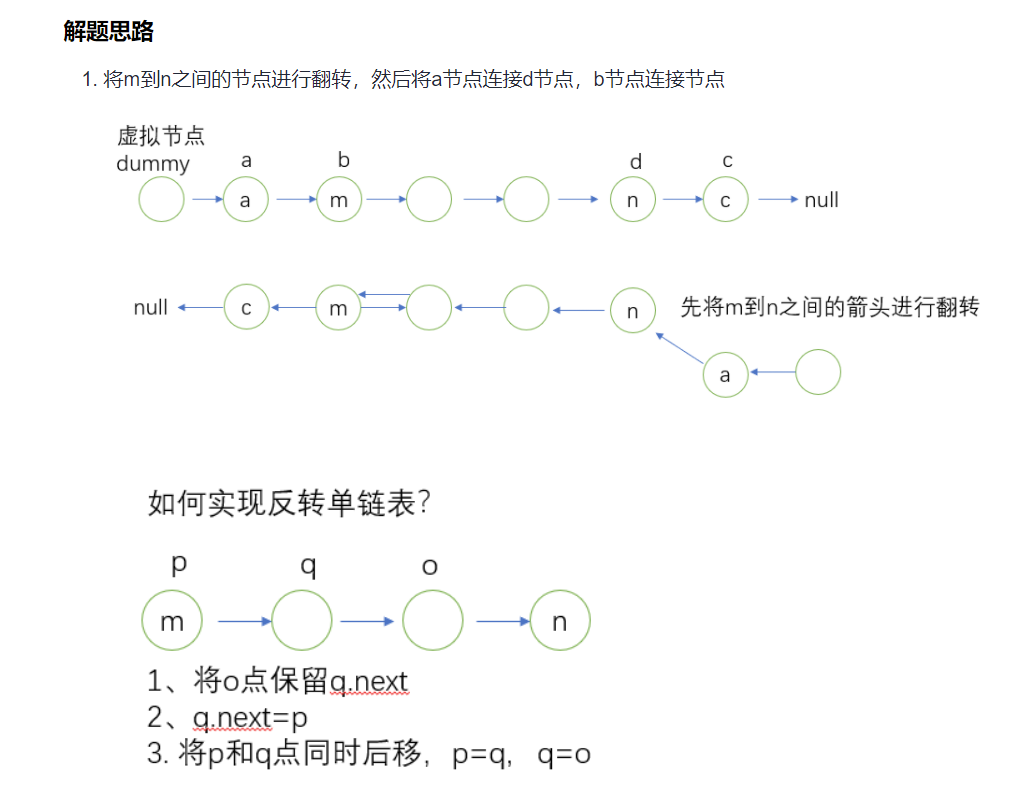
var reverseBetween = function(head, m, n) {
  /**
   * 思路: a 和 d 先移动到指定位置，然后反转链表，最后将 a 指向d,b指向c
   */
  if (m === n) {
    return head;
  }
  let dummyNode = new ListNode(0);
  dummyNode.next = head;
  // 首先让a,d移动到相应的位置
  let a = dummyNode;
  let d = dummyNode;
  for (let i = 0; i < m - 1; i++) {
    a = a.next;
  }
  for (let i = 0; i < n; i++) {
    d = d.next;
  }
  // 反转m到n的链表
  let b = a.next;
  let c = d.next;
  // 这里注意如何反转，定义变量写在条件里面，然后终止条件为p1!==c
  for (let p2 = b, p1 = p2.next; p1 !== c; ) {
    let temp = p1.next;
    p1.next = p2;
    p2 = p1;
    p1 = temp;
  }
  // 将a指向d，m指向c
  a.next = d;
  b.next = c;
  return dummyNode.next;
};

# 链表奇偶重排 (opens new window)

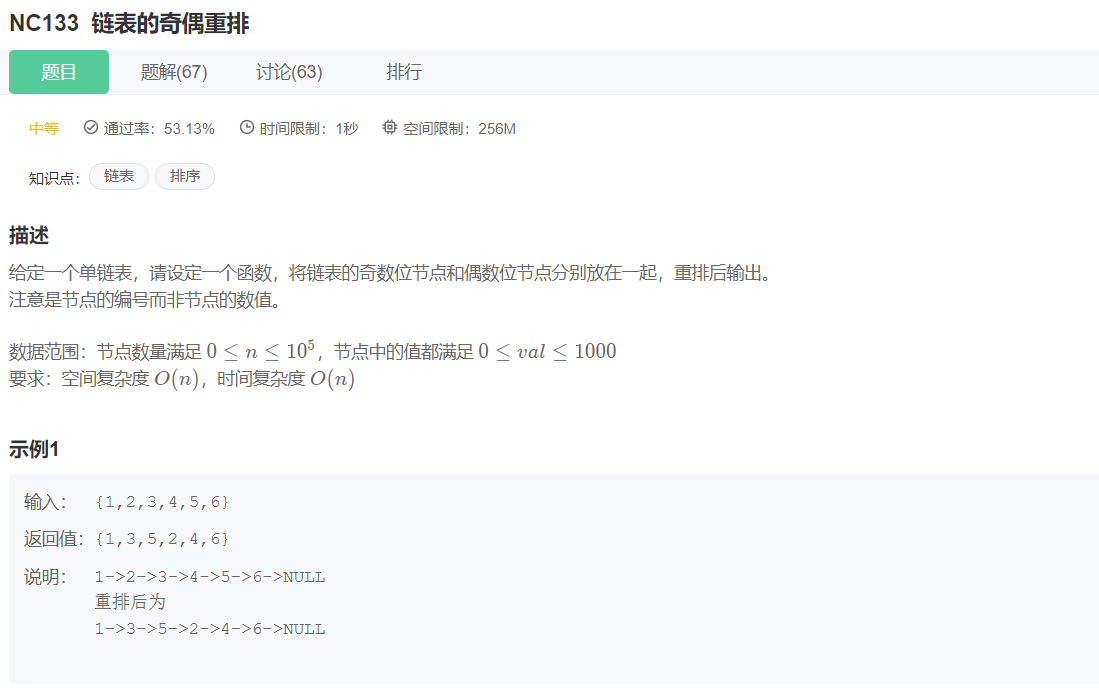
function oddEvenList(head) {
  // write code here
  if (!head) {
    return null;
  }
  let odd = head;
  let even = head.next;
  let evenHead = even; //保存偶数链节点
  // 保证偶数链走下去
  while (even && even.next) {
    // 奇数和偶数下个节点都指向下下个
    odd.next = odd.next.next;
    even.next = even.next.next;
    // 保证遍历下去
    odd = odd.next;
    even = even.next;
  }
  odd.next = evenHead;
  return head;
}

数组变型

直接遍历数组元素，为奇数就和 nums[i]，交换位置

var exchange = nums => {
  let i = 0;
  for (let j = 0; j < nums.length; j++) {
    if (nums[j] % 2 !== 0) {
      let temp = nums[j];
      nums[i] = nums[j];
      nums[j] = temp;
    }
  }
  return nums;
};

# 删除链表中的结点 (opens new window)

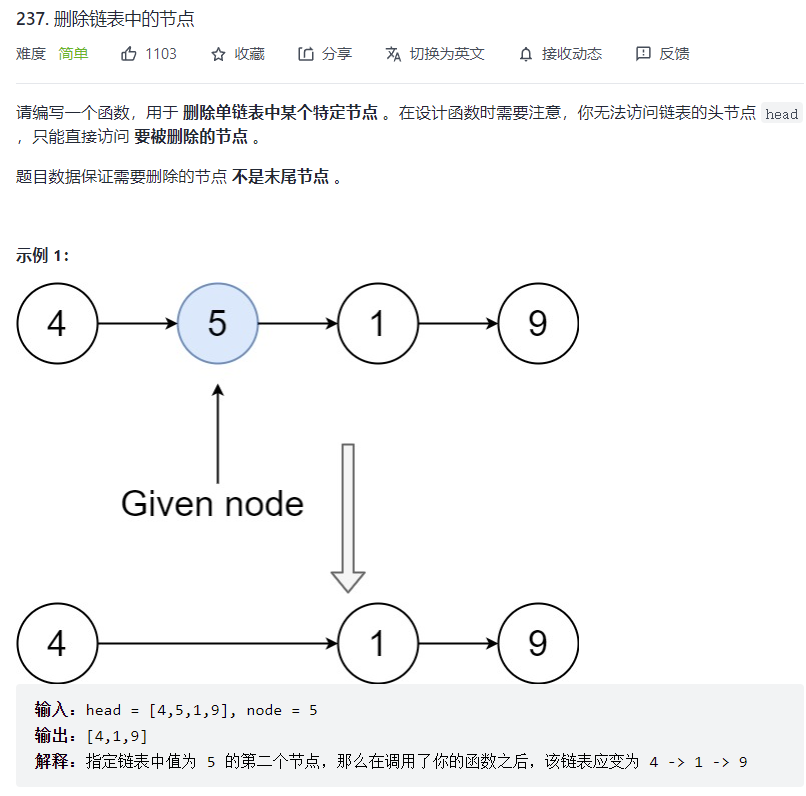
var deleteNode = function(node) {
  node.val = node.next.val;
  node.next = node.next.next;
};

# 删除排序链表中的重复元素 (opens new window)(高频 ❤️❤️❤️)

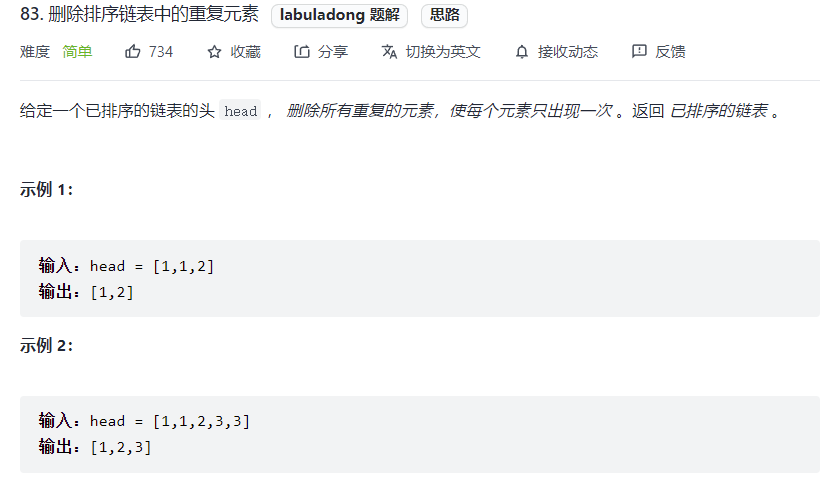
var deleteDuplicates = function(head) {
  let p = head;
  while (p && p.next) {
    // 如果相同 删除
    if (p.val === p.next.val) {
      p.next = p.next.next;
    } else {
      // 遍历下去
      p = p.next;
    }
  }
  return head;
};

# 两数相加 (opens new window)(高频 ❤️❤️❤️)

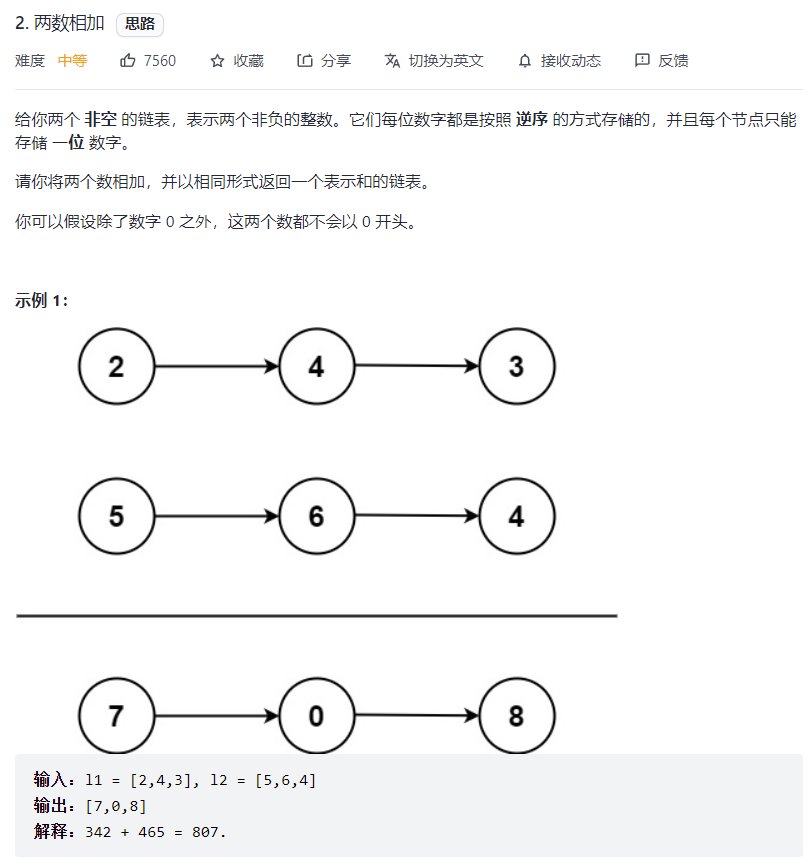
思路就是使用伪结点记录双结点的值相加，但是需要考虑到超过 10 的情况，使用一个变量记录十位上的数，超过十则结点值为除以 10 的余数，最后如果最后一位也超过 10，结点值就是十位上的数。

var addTwoNumbers = function(l1, l2) {
  const l3 = new ListNode(0);
  let p1 = l1;
  let p2 = l2;
  let p3 = l3;
  // 十位上的数，因为可能出现4+7的情况 11
  let carry = 0;
  while (p1 || p2) {
    // 取值
    const v1 = p1 ? p1.val : 0;
    const v2 = p2 ? p2.val : 0;
    const v3 = v1 + v2 + carry;
    carry = Math.floor(v3 / 10);
    p3.next = new ListNode(v3 % 10);
    if (p1) p1 = p1.next;
    if (p2) p2 = p2.next;
    p3 = p3.next;
  }
  // 考虑最后一位可能也会超过10，直接以carry作为结点末尾
  if (carry) {
    p3.next = new ListNode(carry);
  }
  return l3.next;
};

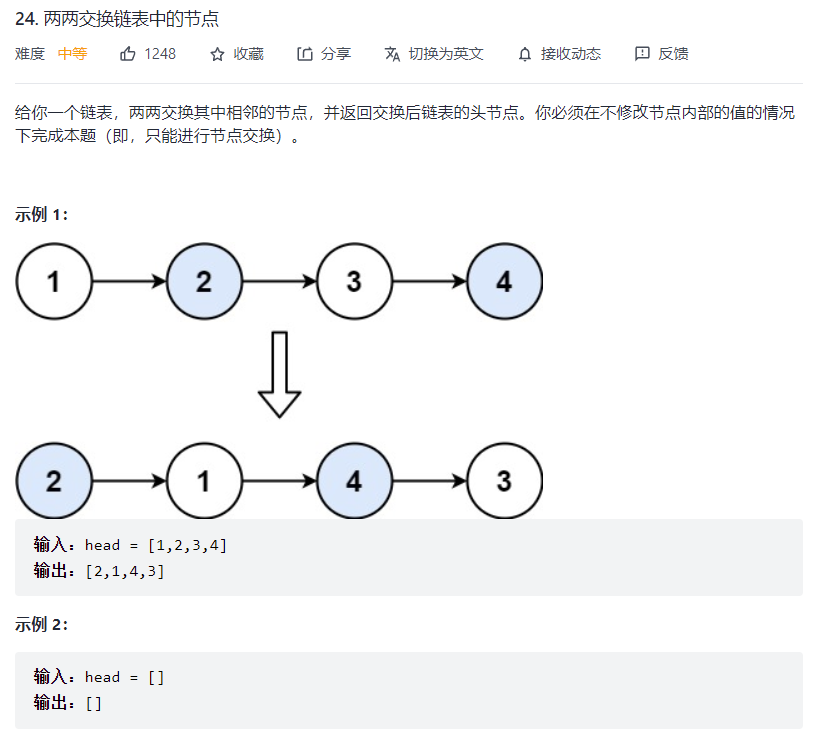
# 两两交换链表中的节点 (opens new window)(高频 ❤️❤️❤️)

https://juejin.cn/post/6844904061947346957#heading-11

var swapPairs = function(head) {
  /**
   * 画图分析，这里node1.next = node2.next,node2.next=node1 需要写在while条件当中，让指针遍历下去
   * p指针的作用: 确定node1和node2的位置
   * 最后返回伪节点.next即可
   */
  if (head == null || head.next == null) return head;
  let dummyHead = (p = new ListNode());
  dummyHead.next = head;
  let node1, node2;
  while ((node1 = p.next) && (node2 = p.next.next)) {
    node1.next = node2.next;
    node2.next = node1;
    p.next = node2;
    p = node1;
  }
  return dummyHead.next;
};

递归版

var swapPairs = function(head) {
  if (head === null || head.next === null) {
    return head;
  }
  let p1 = head;
  let p2 = head.next;
  p1.next = swapPairs(p2.next);
  p2.next = p1;
  return p2;
};

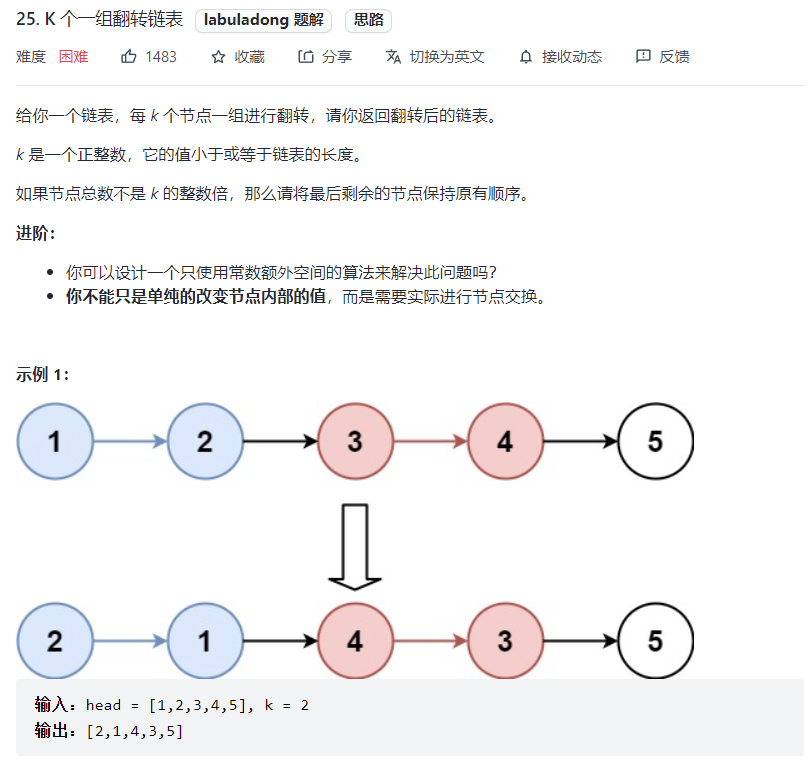
# K 个一组翻转链表 (opens new window)(高频 ❤️❤️❤️)

var reverseKGroup = function(head, k) {
  let pre = null,
    cur = head;
  let p = head;
  // 下面的循环用来检查后面的元素是否能组成一组
  for (let i = 0; i < k; i++) {
    if (p == null) return head;
    p = p.next;
  }
  for (let i = 0; i < k; i++) {
    let next = cur.next;
    cur.next = pre;
    pre = cur;
    cur = next;
  }
  // pre为本组最后一个节点，cur为下一组的起点
  head.next = reverseKGroup(cur, k);
  return pre;
};

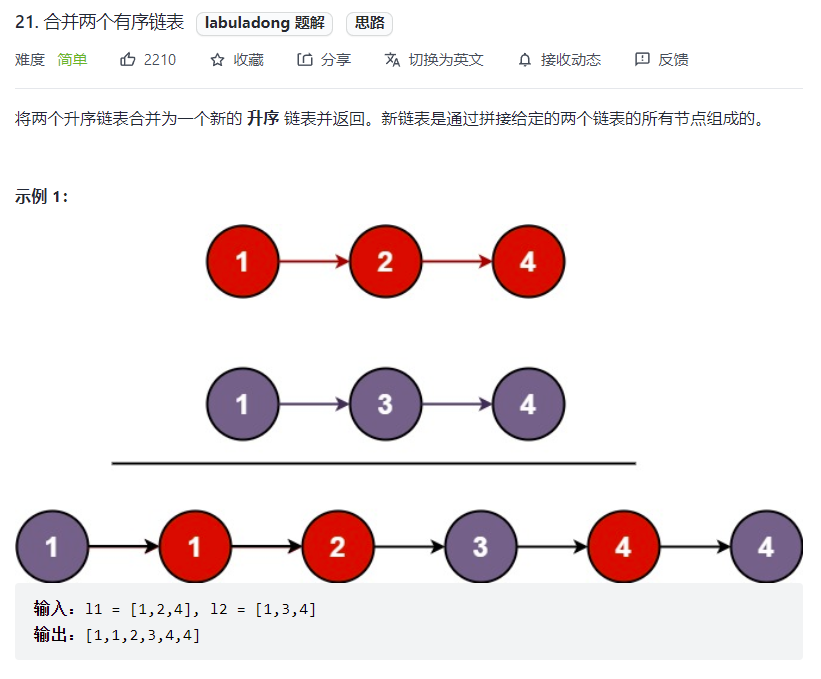
# 合并两个有序链表 (opens new window)(高频 ❤️❤️❤️)

var mergeTwoLists = function(l1, l2) {
  /**
   * 将较小值的链表连接到排序好的链表之后，然后考虑特殊性情况l1,l2为null时的情况
   */
  if (l1 === null) {
    return l2;
  }
  if (l2 === null) {
    return l1;
  }
  if (l1.val > l2.val) {
    l2.next = mergeTwoLists(l1, l2.next);
    return l2;
  } else {
    l1.next = mergeTwoLists(l1.next, l2);
    return l1;
  }
};

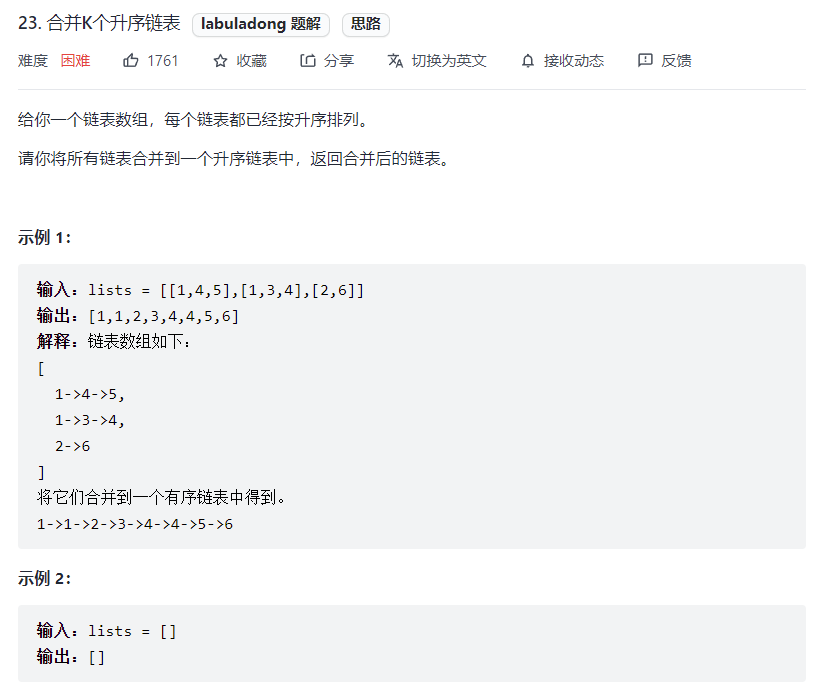
# 合并 k 个有序链表 (opens new window)(高频 ❤️❤️❤️)

var mergeKLists = function(lists) {
  if (!lists.length) {
    return null;
  }
  /**
   * 合并两个有序链表，然后两两合并k个链表
   */
  var mergeTwoList = (l1, l2) => {
    if (l1 === null) {
      return l2;
    }
    if (l2 === null) {
      return l1;
    }
    if (l1.val < l2.val) {
      l1.next = mergeTwoList(l1.next, l2);
      return l1;
    } else {
      l2.next = mergeTwoList(l1, l2.next);
      return l2;
    }
  };
  let res = lists[0];
  for (let i = 1; i < lists.length; i++) {
    // 存在lists[i] 时，进行两两合并
    if (lists[i]) {
      res = mergeTwoList(res, lists[i]);
    }
  }
  return res;
};

# 复杂链表的复制 (opens new window)

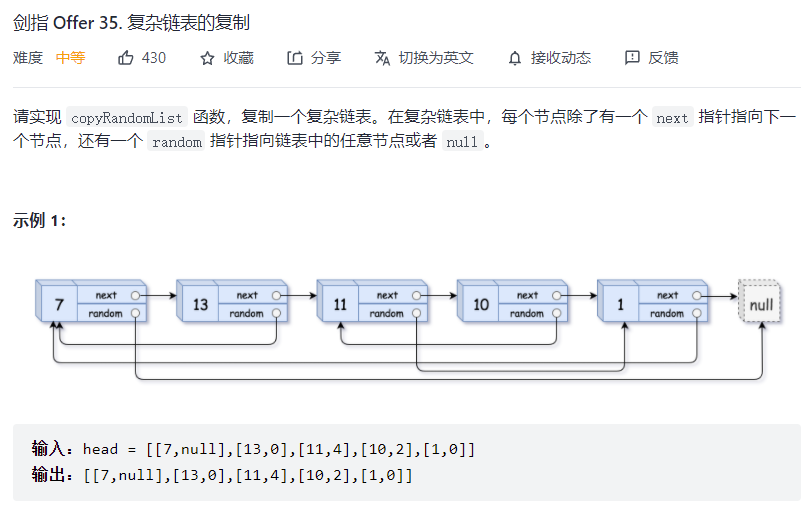
var copyRandomList = function(head) {
  /**
   * 思路：使用哈希表完成链表的深拷贝，先把链表节点放入哈希表，一定要对next和random指针进行判空
   */
  let map = new Map();
  // 保存链表
  let node = head;
  while (node) {
    map.set(node, new Node(node.val));
    node = node.next;
  }
  // 判空
  node = head;
  while (node) {
    // node节点的next和random判空
    map.get(node).next = node.next ? map.get(node.next) : null;
    map.get(node).random = node.random ? map.get(node.random) : null;
    node = node.next;
  }
  return map.get(head);
};

# 重排链表 (opens new window)(高频 ❤️❤️❤️)

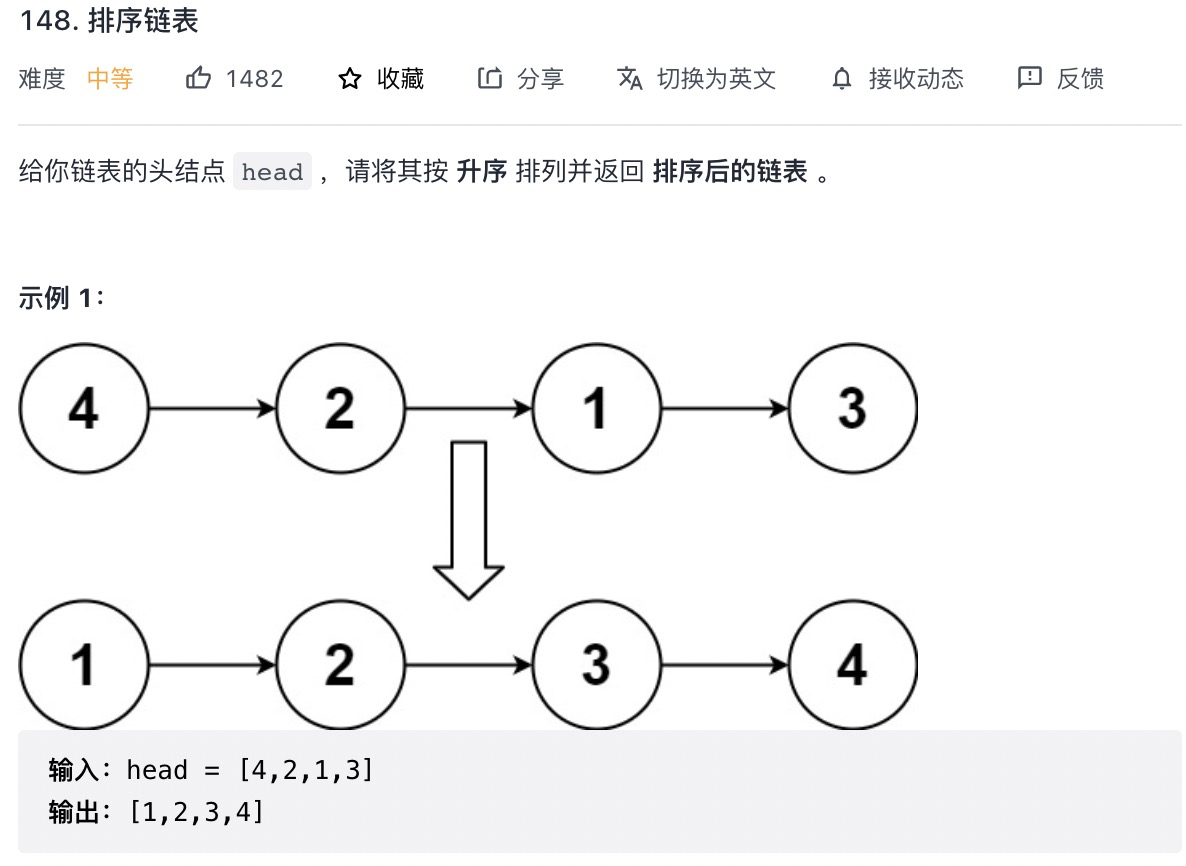
# 排序链表 (opens new window)(高频 ❤️❤️❤️)

# 双指针

# 环形链表 (opens new window)(高频 ❤️❤️❤️)

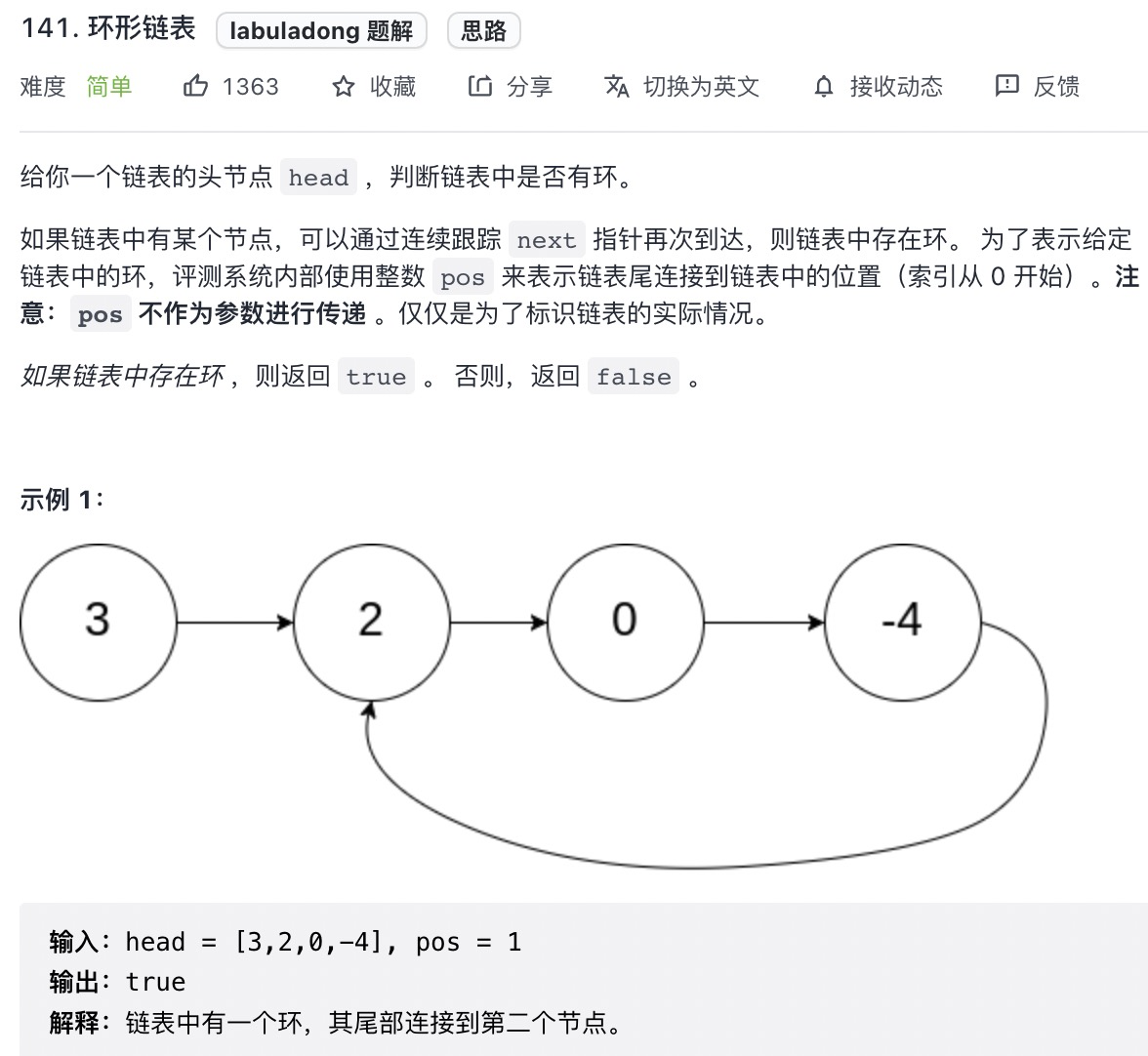
快慢指针

var hasCycle = function(head) {
  let fast = head;
  let slow = head;
  while (fast && fast.next) {
    slow = slow.next;
    fast = fast.next.next;
    if (fast === slow) {
      return true;
    }
  }
  return false;
};

# 求双链表的第一个公共结点 (opens new window)(高频 ❤️❤️❤️)

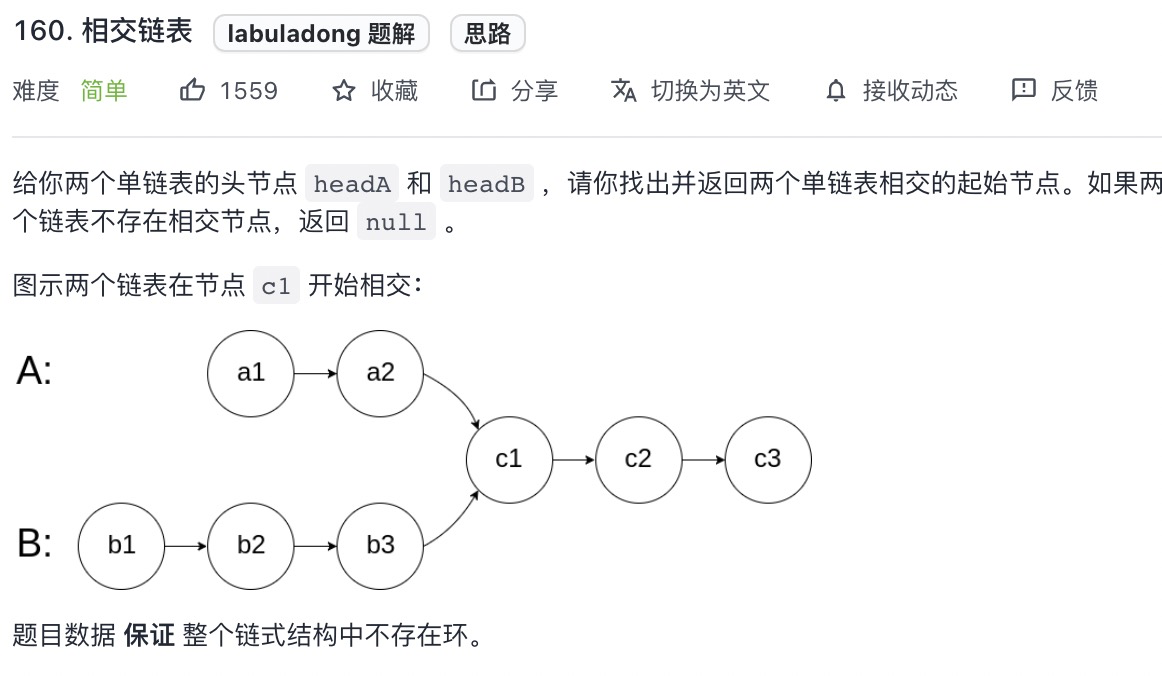
思路：定义双指针，同时遍历，需要保证双指针都有值，如果没有值就为初始值

var getIntersectionNode = function(headA, headB) {
  let p1 = headA;
  let p2 = headB;
  while (p1 !== p2) {
    p1 = p1 ? p1.next : headA;
    p2 = p2 ? p2.next : headB;
  }
  return p1;
};

# 环形链表 II (opens new window)(高频 ❤️❤️❤️)

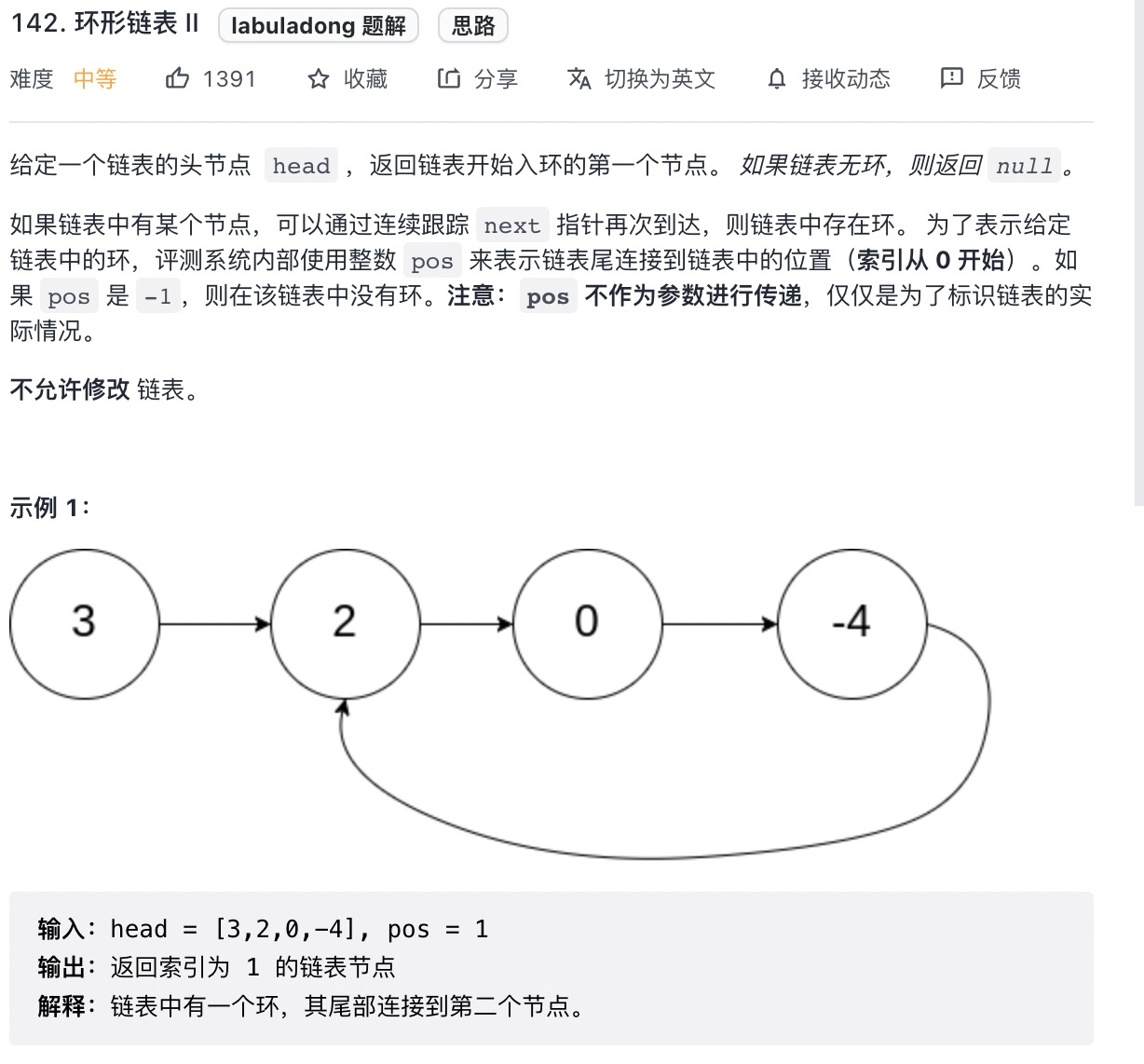
快慢指针

var detectCycle = function(head) {
  // 首先快指针和满指针先成环，跑一圈
  let fast = head;
  let slow = head;
  while (fast && fast.next) {
    fast = fast.next.next;
    slow = slow.next;
    if (fast === slow) {
      break;
    }
  }
  // 如果没有成环
  if (!fast || !fast.next) {
    return null;
  }
  // 然后再匀速跑,再次相遇就是第一个入环的结点
  slow = head;
  while (fast !== slow) {
    fast = fast.next;
    slow = slow.next;
  }
  return slow;
};

# 链表的中间结点 (opens new window)(高频 ❤️❤️❤️)

快慢指针

var middleNode = function(head) {
  let fast = head;
  let slow = head;
  while (fast && fast.next) {
    fast = fast.next.next;
    slow = slow.next;
    console.log("head", head, "fast", fast, "slow", slow);
  }
  return slow;
};

# 删除链表的倒数第 N 个结点 (opens new window)(高频 ❤️❤️❤️)

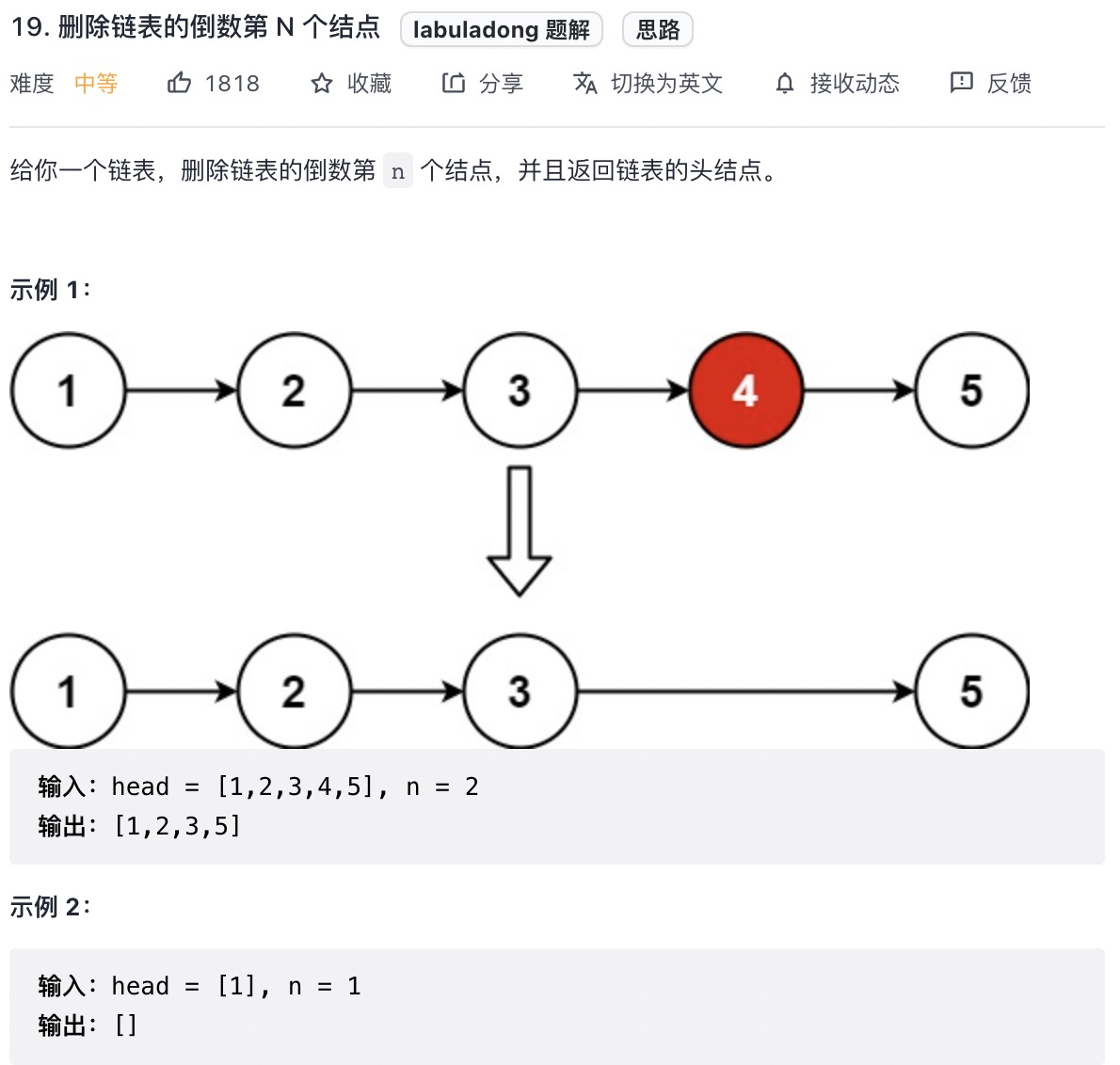
快慢指针

var removeNthFromEnd = function(head, n) {
  let fast = head;
  let slow = head;
  // 快指针先走n步
  for (let i = 0; i < n; i++) {
    fast = fast.next;
  }
  // 如果删除的倒数第n个结点是头结点，直接返回下一结点
  if (fast === null) {
    return head.next;
  }
  // 快指针走完之后双指针匀速前行，到头则slow.next就是要删除的倒数第n个结点
  while (fast && fast.next) {
    fast = fast.next;
    slow = slow.next;
  }
  slow.next = slow.next.next;
  return head;
};

# 回文链表 (opens new window)(高频 ❤️❤️❤️)

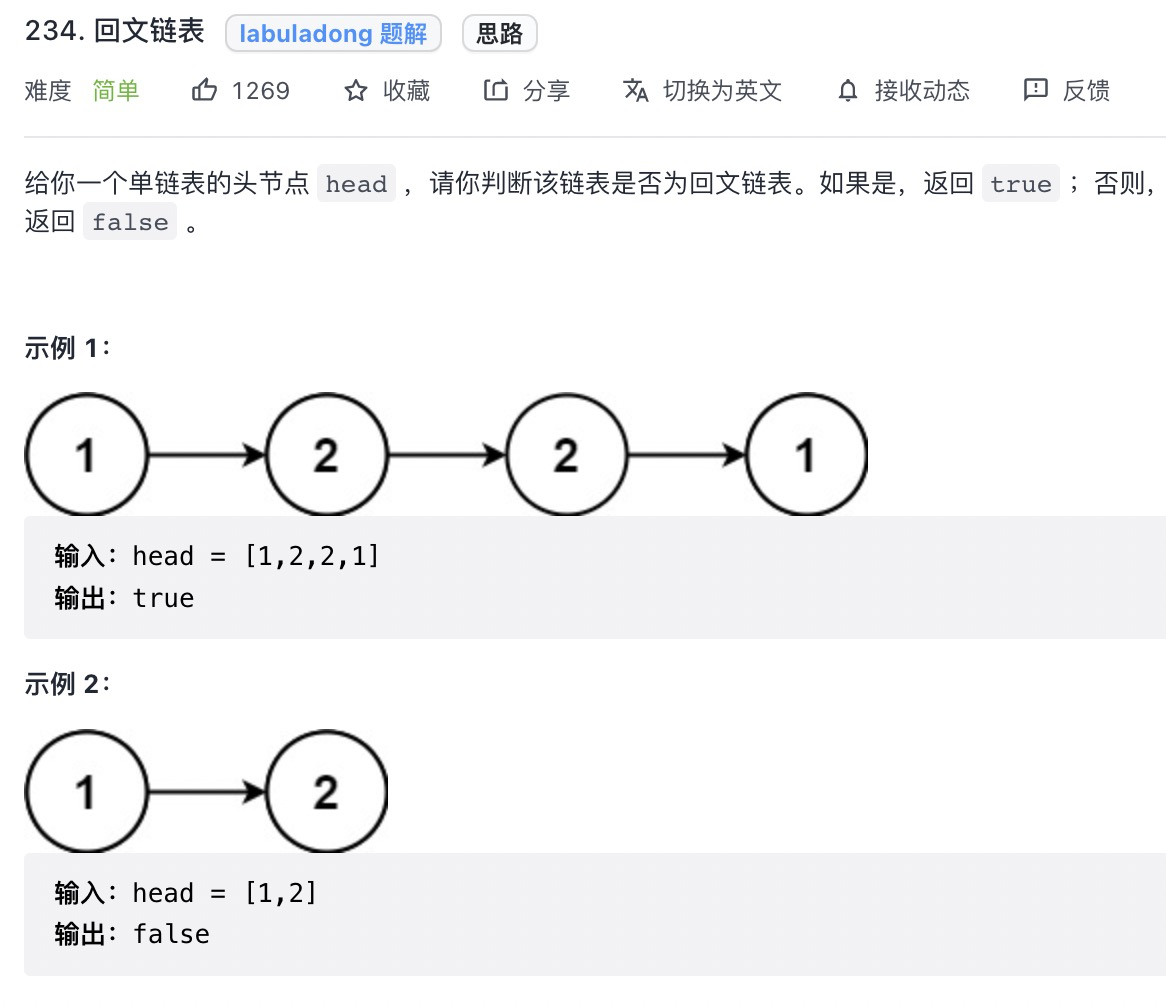
思路: 1.拿到后半部分链表 2.反转链表 3.和原链表进行比对

var isPalindrome = function(head) {
  /**
   * 1. 快满指针获取中间结点
   * 2. 反转中间结点之后的结点
   * 3. 遍历后半部分结点，一一比对前后链表的值，head=head.next reverseHead = reverseHead.next
   * 4. 相同返回true，否则返回false
   */
  if (!head) {
    return true;
  }
  let fast = head;
  let slow = head;
  while (fast.next && fast.next.next) {
    fast = fast.next.next;
    slow = slow.next;
  }
  // 将中间结点之后的结点反转
  let reverseHead = reverseList(slow.next);
  while (reverseHead) {
    if (head.val !== reverseHead.val) {
      return false;
    }
    reverseHead = reverseHead.next;
    head = head.next;
  }
  return true;
  function reverseList(head) {
    let p1 = head;
    let p2 = null;
    while (p1) {
      const temp = p1.next;
      p1.next = p2;
      p2 = p1;
      p1 = temp;
    }
    return p2;
  }
};

# 反转字符串 (opens new window)

前后指针

var reverseString = function(s) {
  let left = 0;
  let right = s.length - 1;
  while (left < right) {
    const temp = s[left];
    s[left] = s[right];
    s[right] = temp;
    left++;
    right--;
  }
};

# 判断回文字符串(高频 ❤️❤️❤️)

function isPalindrome(s) {
  let left = 0;
  let right = s.length - 1;
  while (left < right) {
    if (s[left] !== s[right]) return false;
    left++;
    right--;
  }
  return true;
}

# 合并两个有序数组 (opens new window)(高频 ❤️❤️❤️)

var merge = function(nums1, m, nums2, n) {
  /**
   * 用三个指针解决这个问题，假设数组1，数组2，待填充数组1
   * i,j,k 分别表示他们的尾步 m-1 n-1 nums1.length-1
   * 1. 如果i,j都有值，则nums1[k] = 更大的值，指针往前移
   * 2. 如果 i 指针循环完了，j 指针的数组里还有值未处理的话，直接从 k 位置开始向前填充 j 指针数组即可。因为此时数组 1 原本的值一定全部被填充到了数组 1 的后面位置，且这些值一定全部大于此时 j 指针数组里的值。
   *
   */
  let i = m - 1;
  let j = n - 1;
  let k = nums1.length - 1;
  while (i >= 0 && j >= 0) {
    if (nums1[i] > nums2[j]) {
      nums1[k] = nums1[i];
      i--;
    } else {
      nums1[k] = nums2[j];
      j--;
    }
    k--;
  }
  // i循环完成,直接从k开始填充nums2[j]
  while (j >= 0) {
    nums1[k] = nums2[j];
    j--;
    k--;
  }
};

# 通过删除字母匹配到字典里最长单词 (opens new window)

var findLongestWord = function(s, d) {
  /**
   * 思路：使用双指针，题意是d中的哪个元素存在s，并且这个元素的长度是最大的，如果有多个就比较字典顺序。
   * 这里使用双指针一个遍历s，一个d的每个元素。如果s[i] === w[j]，指针往前移动，这里也需要注意有一种情况是不需要移动的，已匹配数量 + 剩余字符个数 <= maxL，这里就不需要继续匹配
   *
   * 讲的很绕，其实看代码就看的懂，原理就是维护双指针
   */

  // 找到d中存在于s的字符的字符最大数量
  let find = (s, w, max) => {
    // 维护s和w指针
    let i = 0;
    let j = 0;
    let count = 0;
    // 已匹配字符数量 + 剩余字符数量 >= max 才进行匹配
    while (i < s.length && j < w.length && count + w.length - j >= max) {
      // 找到一个字符 就前移w指针
      if (s[i] === w[j]) {
        j++;
        count++;
      }
      i++;
    }
    // 最后w.length = count,代表匹配完成
    if (w.length === count) {
      return count;
    } else {
      return 0;
    }
  };

  let maxL = 0;
  let index = -1;
  for (let i = 0; i < d.length; i++) {
    let curCount = find(s, d[i], maxL);
    // 1.当前匹配字符数量大于最大值 2. 当前匹配数量等于最大值，更新字典顺序小的
    // 更新maxL和index
    if (curCount > maxL || (maxL === curCount && d[index] > d[i])) {
      maxL = curCount;
      index = i;
    }
  }
  return !!d[index] ? d[index] : "";
};

# 盛最多水的容器 (opens new window)(高频 ❤️❤️❤️)

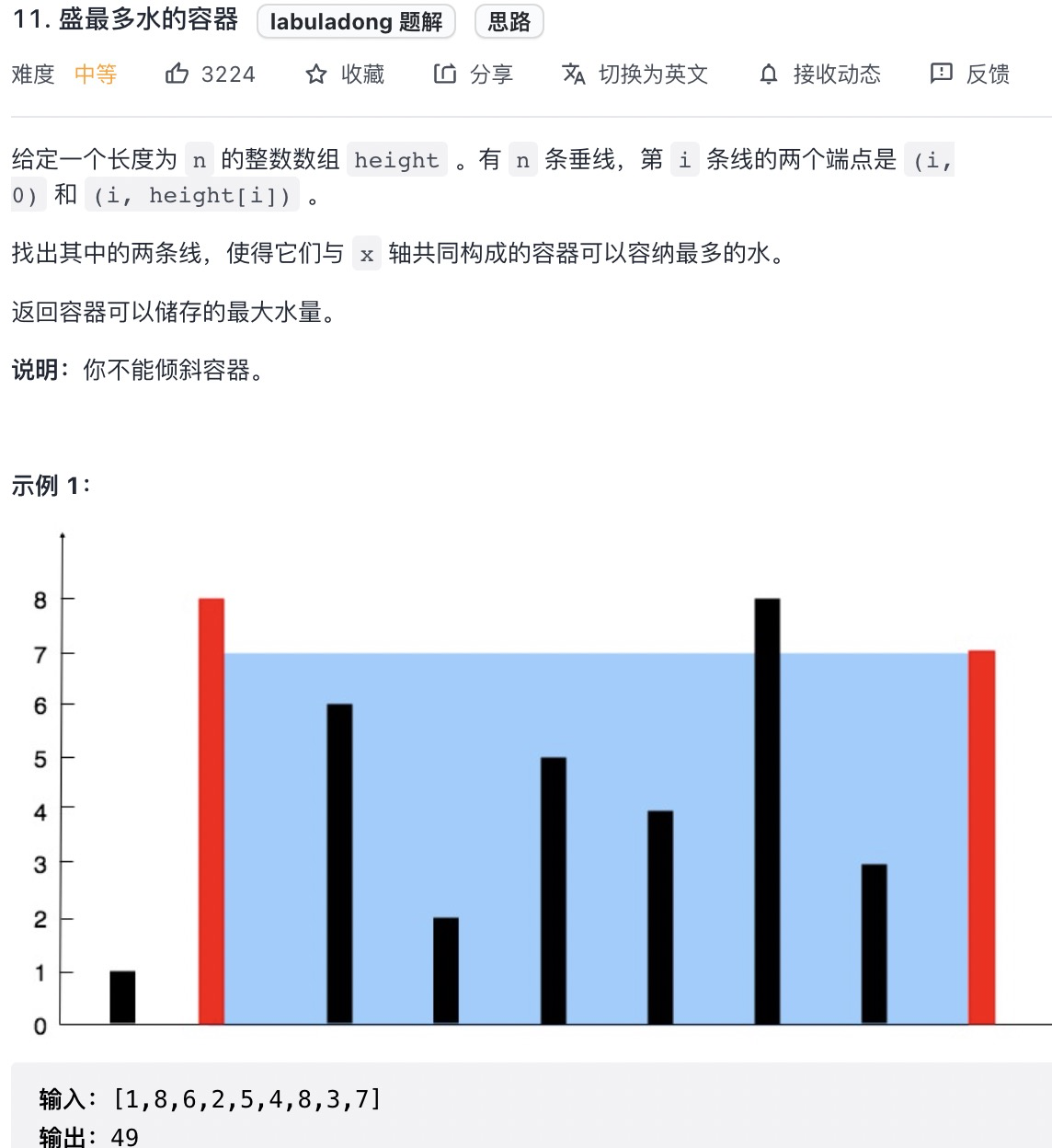
var maxArea = function(height) {
  /**
   * 双指针法：
   * 1. 如果左指针的高度小于右指针的话，也就是左边低右边高，这是时候面积 = 左高*(右减左),左指针移动
   * 2. 右指针高度小于左指针，面积=右高度*(左减右),右指针缩小
   * 每次更新最后的返回值
   */
  if (!height) return 0;
  let res = 0;
  let left = 0;
  let right = height.length - 1;
  while (left < right) {
    if (height[left] <= height[right]) {
      let curArea = height[left] * (right - left);
      res = Math.max(res, curArea);
      left++;
    } else {
      let curArea = height[right] * (right - left);
      res = Math.max(res, curArea);
      right--;
    }
  }
  return res;
};

# 接雨水 (opens new window)(高频 ❤️❤️❤️)

var trap = function(height) {
  /**
   * 当前单元格能够存放的水量 = (左边单元格高度最大值 - 当前单元格高度)
   * 双指针
   */
  let left = 0;
  let leftHeight = 0;
  let right = height.length - 1;
  let rightHeight = 0;
  let res = 0;
  while (left < right) {
    if (height[left] < height[right]) {
      leftHeight = Math.max(height[left], leftHeight);
      res += leftHeight - height[left];
      left++;
    } else {
      rightHeight = Math.max(height[right], rightHeight);
      res += rightHeight - height[right];
      right--;
    }
  }
  return res;
};

# 二叉树

计算二叉树的时间复杂度：https://www.jianshu.com/p/f5cc8b2f207c

# 遍历系列

# 二叉树的层序遍历 (opens new window)(高频 ❤️❤️❤️)

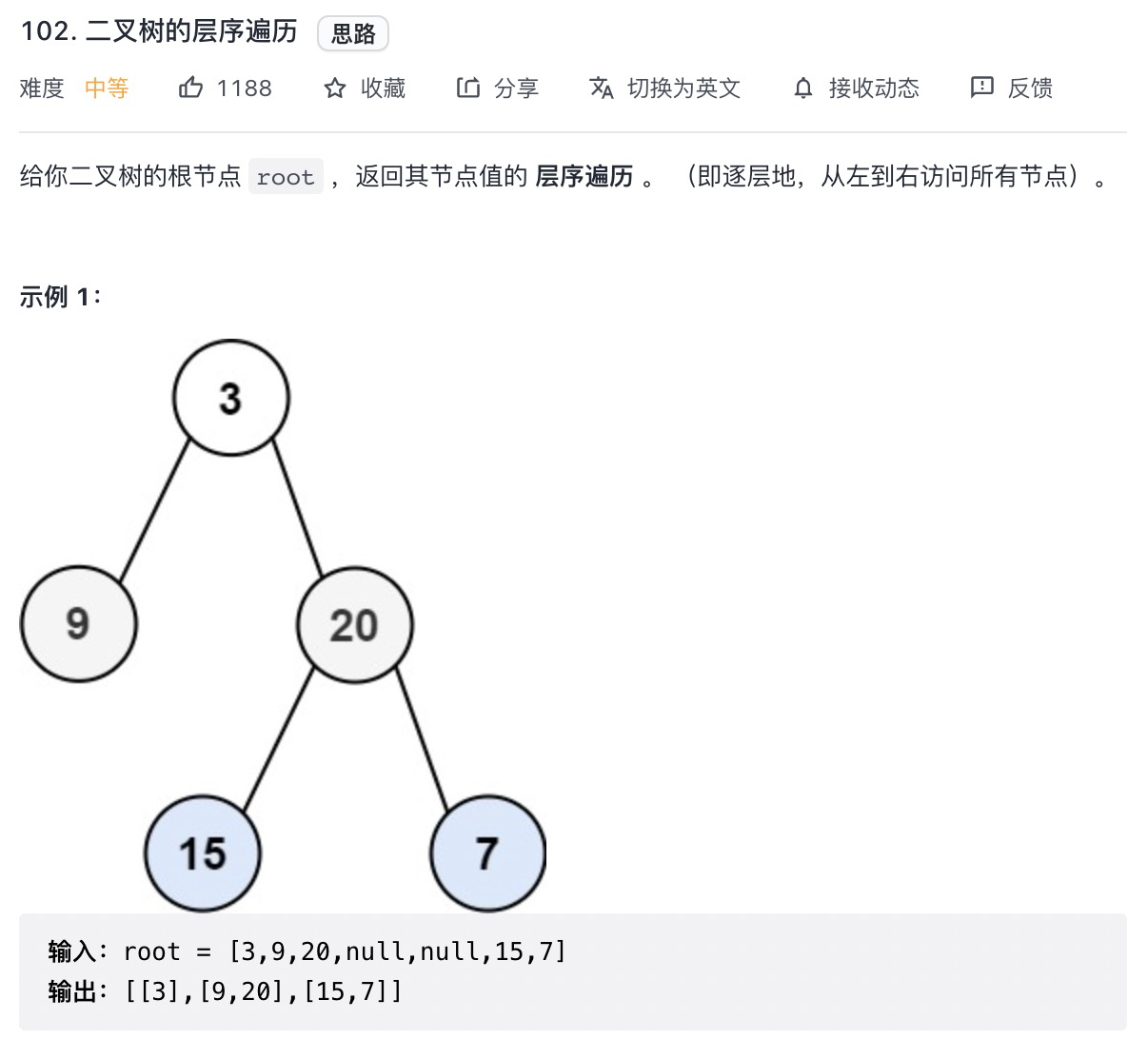
var levelOrder = function(root) {
  if (!root) {
    return [];
  }
  let q = [root];
  let res = [];
  // let last
  while (q.length) {
    let size = q.length;
    let levelList = [];
    for (let i = 0; i < size; i++) {
      let n = q.shift();
      if (n.left) {
        q.push(n.left);
      }
      if (n.right) {
        q.push(n.right);
      }
      if (n !== undefined) {
        // last = n.val// 用变量只能保存到最后一个节点
        levelList.push(n.val);
      }
    }
    res.push(levelList);
  }
  return res;
};

# 二叉树的中序遍历 (opens new window)(高频 ❤️❤️❤️)

var inorderTraversal = function(root) {
  let res = [];
  // 递归版本   let innerorder = (root)=>{
  //       if(!root){
  //           return
  //       }
  //       innerorder(root.left)
  //       res.push(root.val)
  //       innerorder(root.right)
  //   }
  //   innerorder(root)

  // 非递归版本
  let p = root;
  let stack = [];
  while (stack.length || p) {
    // 拿到所有的左节点
    while (p) {
      stack.push(p);
      p = p.left;
    }
    // 弹出节点尽头，并访问
    const n = stack.pop();
    res.push(n.val);
    // 取右节点
    p = n.right;
  }
  return res;
};

# 二叉树的锯齿形层序遍历 (opens new window)(高频 ❤️❤️❤️)

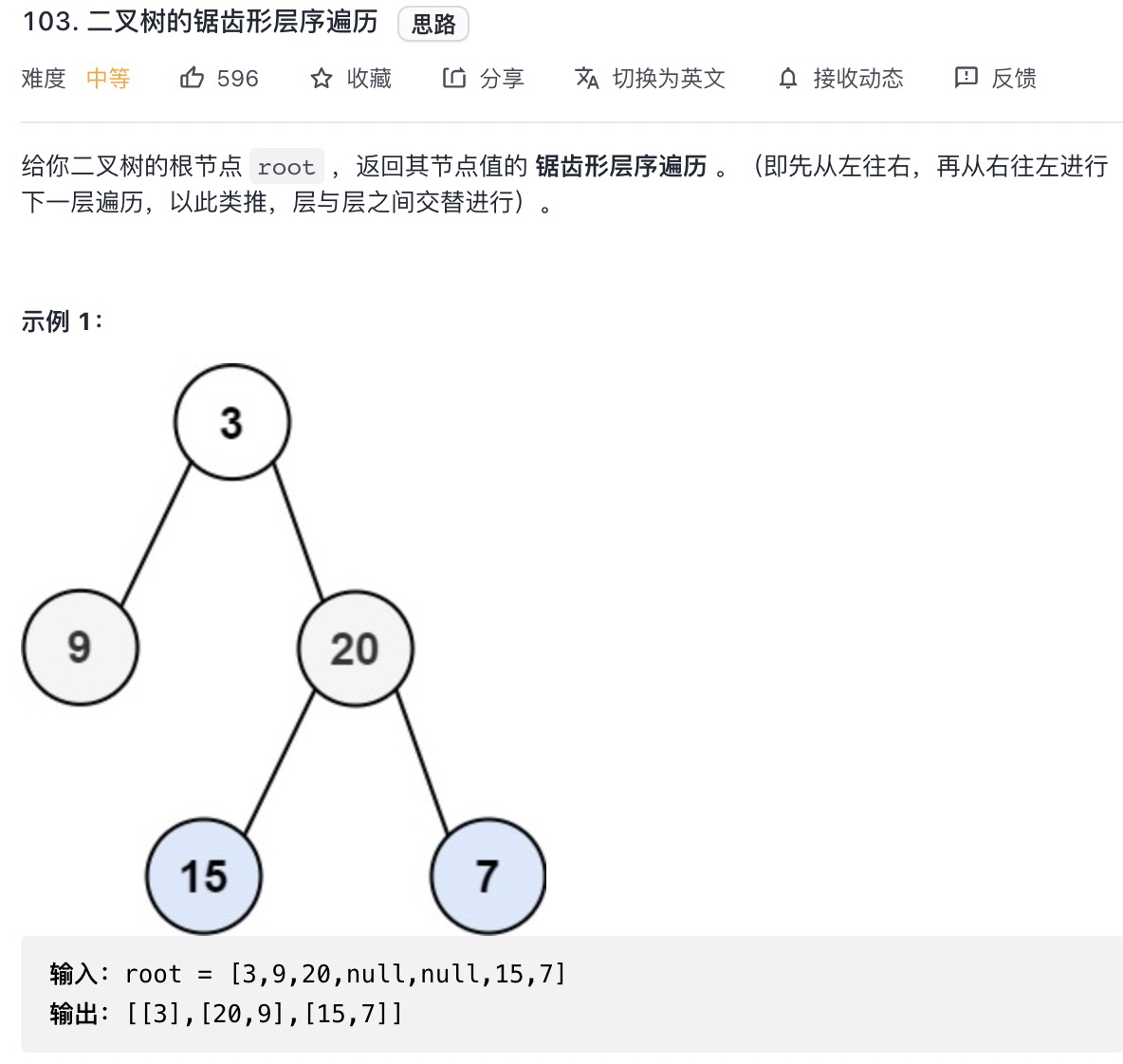
var zigzagLevelOrder = function(root) {
  /**
   * 思路：这道题的102层次遍历类似，只是说一层从左往右遍历一层从右往左,这个可以使用一个便变量控制,最后一个是push到层级数组，一个是unshift到层级数组，顺序不一样
   */
  if (!root) {
    return [];
  }
  let q = [root];
  let isLeftToRight = true;
  let res = [];
  while (q.length) {
    let levelList = [];
    let size = q.length;
    for (let i = 0; i < size; i++) {
      let node = q.shift();
      if (node.left) {
        q.push(node.left);
      }
      if (node.right) {
        q.push(node.right);
      }
      if (node !== undefined && isLeftToRight) {
        levelList.push(node.val);
      } else {
        levelList.unshift(node.val);
      }
    }
    res.push(levelList);
    isLeftToRight = !isLeftToRight;
  }
  return res;
};

# 已知二叉树求某值

# 二叉树的最小深度 (opens new window)(高频 ❤️❤️❤️)

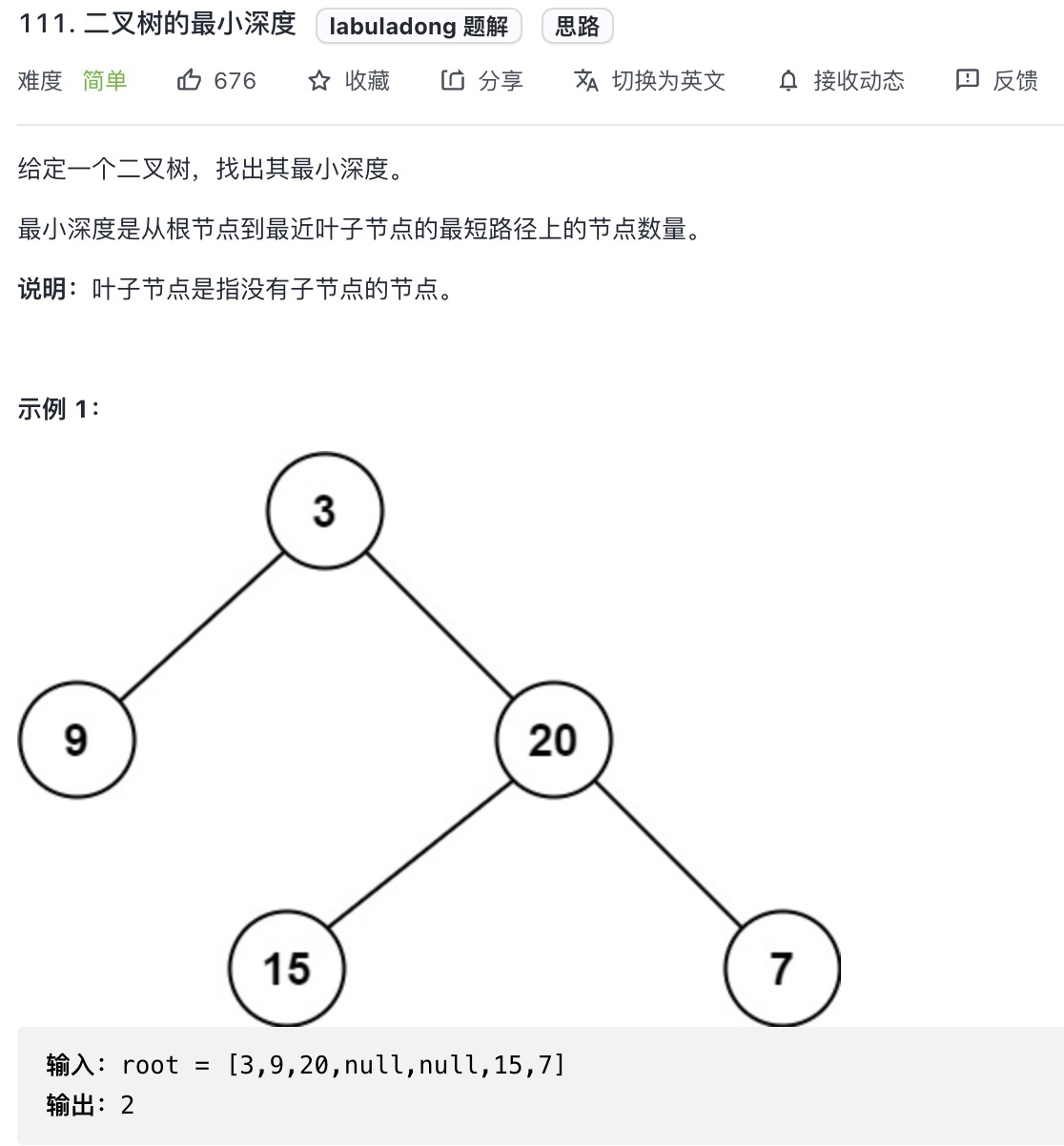
var minDepth = function(root) {
  /**
   * 二叉树的最小深度：
   * dfs：即在每次dfs的过程中更新最小结果
   * bfs：标准bfs格式，只需要引入depth，每次遍历累加，最后返回深度
   * */
  // dfs  if(!root){return 0}
  //   if(!root.left && !root.right){
  //       return 1
  //   }
  //   let res = Number.MAX_VALUE
  //   if(root.left){
  //       res = Math.min(minDepth(root.left),res)
  //   }
  //   if(root.right){
  //       res = Math.min(minDepth(root.right),res)
  //   }
  //   return res + 1

  // bfs 将结点和depth当成数组 然后遍历队列，当访问叶子结点时，返回depth
  if (!root) {
    return 0;
  }
  let q = [[root, 1]];
  while (q.length) {
    // 取队头
    let [n, depth] = q.shift();
    if (!n.left && !n.right) {
      return depth;
    }
    if (n.left) {
      q.push([n.left, depth + 1]);
    }
    if (n.right) {
      q.push([n.right, depth + 1]);
    }
  }
};

# 二叉树的直径 (opens new window)(高频 ❤️❤️❤️)

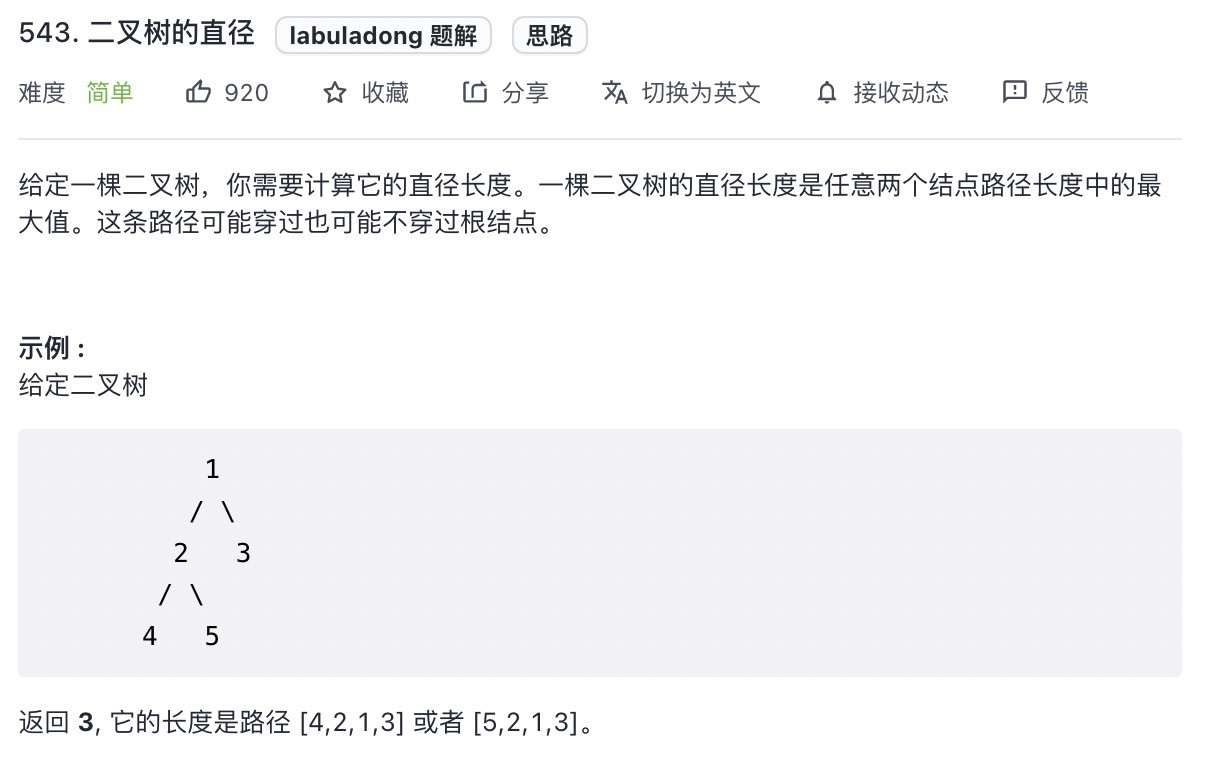
var diameterOfBinaryTree = function(root) {
  /**
   * 思路：题目之意在于让我们求一棵树的左子树的高度+右子树的高度是不是较左子树高度或者右子树高度里最大的
   * 所以我们需要求出左右子树的高度
   * 子树高度：1+Math.max(height(node.left),height(node.right))
   */
  function height(node) {
    if (!node) {
      return 0;
    }
    return 1 + Math.max(height(node.left), height(node.right));
  }
  if (!root) {
    return 0;
  }
  // 处理跟节点为顶点的直径
  let directPath = height(root.left) + height(root.right);
  // 最后返回值需要考虑根节点的左右子节点为顶点的直径，最后取出最大值即可
  return Math.max(directPath, diameterOfBinaryTree(root.left), diameterOfBinaryTree(root.right));
};

# 二叉树的深度 (opens new window)(高频 ❤️❤️❤️)

var maxDepth = function(root) {
  /**
   * 思路：求二叉树的高度：1 + Math.max(height(root.left),height(root.right))
   * */
  if (!root) {
    return 0;
  }
  return 1 + Math.max(maxDepth(root.left), maxDepth(root.right));
  // let res = 0
  // let dfs = (root,l)=>{
  //       if(!root){
  //             return
  //         }
  //     if(!root.left && !root.right && l){
  //         res = Math.max(res,l)
  //     }
  //     if(root.left){
  //        dfs(root.left,l+1)
  //     }
  //     if(root.right){
  //         dfs(root.right,l+1)
  //     }
  // }
  // dfs(root,1)
  // return res
};

# 二叉树的最近公共祖先 (opens new window)(高频 ❤️❤️❤️)

var lowestCommonAncestor = function(root, p, q) {
  /**
     * 思路： 题意让我们找寻pq节点的最近祖先，只要有一个节点等于p或者q，则祖先就是自己，这也是递归结束的条件
     * 有以下情况需要考虑：
     * 1. 当q,p在root左右侧
     * 2. 当q,p在root左右子树的左右侧
     * 
    /
    /**
     * 首先考虑p和q在root节点左右侧 
     *  */
  if (!root) {
    return null;
  }
  // 当根节点有一个等于p或者q，祖先就是root
  if (root === p || root === q) {
    return root;
  }
  /**
   * 继续考虑p和q分别在root节点左子树的两侧，或者右子树的两侧
   */
  let left = lowestCommonAncestor(root.left, p, q);
  let right = lowestCommonAncestor(root.right, p, q);
  // 当左子树结果为null，则pq的祖先在右子树第一个节点，反之同理
  if (!left) return right;
  if (!right) return left;
  // 当pq都不在左右子树，就分布在root左右侧
  return root;
};

# 左叶子之和 (opens new window)(高频 ❤️❤️❤️)

var sumOfLeftLeaves = function(root) {
  /**
   * 思路：利用dfs，首先判断节点是否是叶子节点，然后使用dfs遍历左右子树去，计算左叶子节点的和
   */
  let sum = 0;
  // 判断是否是叶子
  let isLeafNode = node => {
    return node && !node.left && !node.right;
  };
  let dfs = node => {
    // 递归终止条件
    if (!node) {
      return;
    }
    if (isLeafNode(node.left)) {
      sum += node.left.val;
    }
    // 遍历左右子树
    dfs(node.left);
    dfs(node.right);
  };
  dfs(root);
  return sum;
};

# 二叉树的右视图 (opens new window)(高频 ❤️❤️❤️)

var rightSideView = function(root) {
  /**
   * 二叉树的右视图，也就是求每一层遍历的最右边的节点
   * 获取每一层的最右侧节点方法：BFS每次遍历的队列对头元素，如果没有左右子节点并且不等于undefined则他就是这一层的最右节点
   *
   */
  if (!root) {
    return [];
  }
  let res = [];
  let q = [root];
  while (q.length) {
    let len = q.length;
    let last;
    // 获取到BFS每一层的最右侧节点
    for (let i = 0; i < len; i++) {
      let n = q.shift();
      if (n.left) {
        q.push(n.left);
      }
      if (n.right) {
        q.push(n.right);
      }
      if (n !== undefined) {
        last = n.val;
      }
    }
    res.push(last);
  }
  return res;
};

# 二叉搜索树中第 K 小的元素 (opens new window)

var kthSmallest = function(root, k) {
  /**
   * 思路：使用中序遍历，第k小的元素就是当k等于0时的取值
   */
  if (!root) {
    return;
  }
  let p = root;
  let stack = [];
  while (stack.length || p) {
    while (p) {
      stack.push(p);
      p = p.left;
    }
    const n = stack.pop();
    if (--k === 0) {
      return n.val;
    }
    p = n.right;
  }
};

# 特殊的二叉树

# 翻转二叉树 (opens new window)(高频 ❤️❤️❤️)

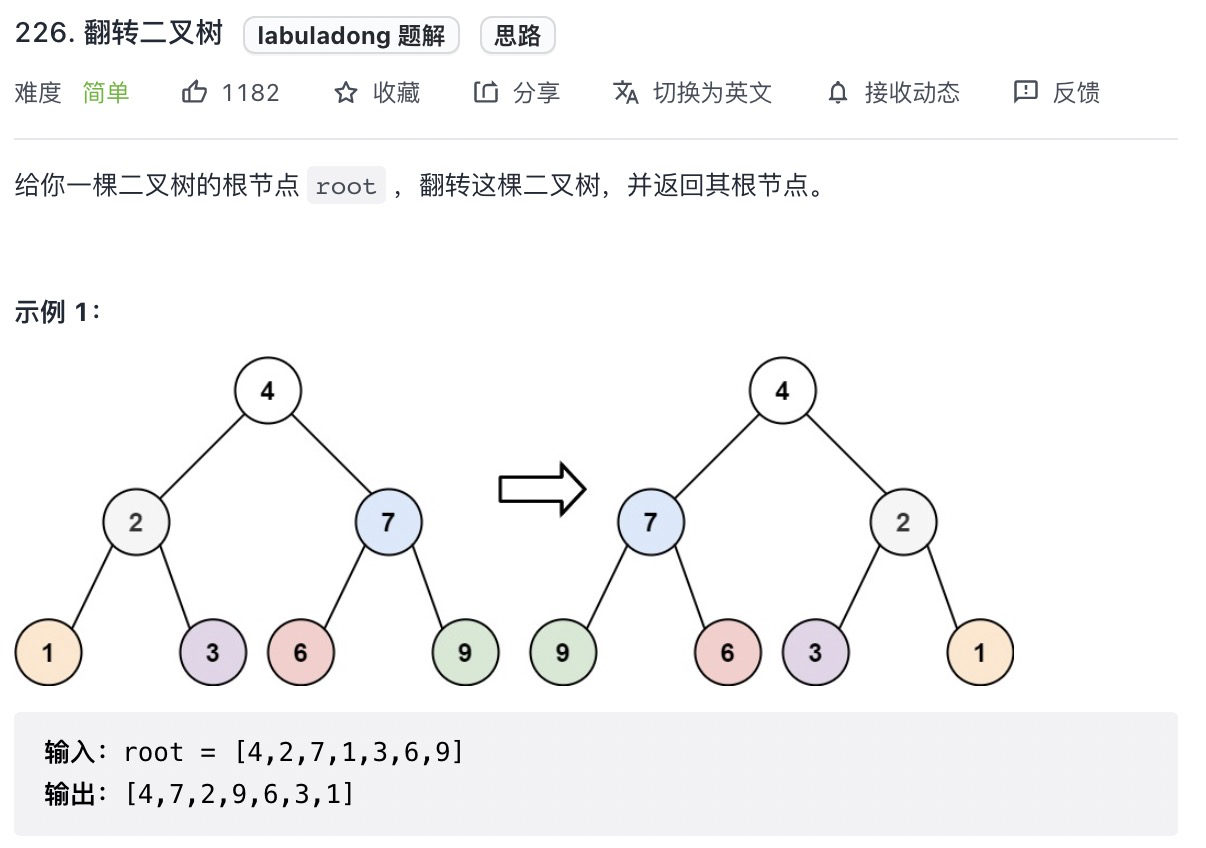
var invertTree = function(root) {
  /**
   * 需要将根节点下的左右子树建换位置即可，类似于dfs
   */
  if (!root) {
    return null;
  }
  [root.left, root.right] = [root.right, root.left];
  /**
   * 左右子树继续翻转
   */
  invertTree(root.left);
  invertTree(root.right);
  return root;
};

# 对称二叉树 (opens new window)(高频 ❤️❤️❤️)

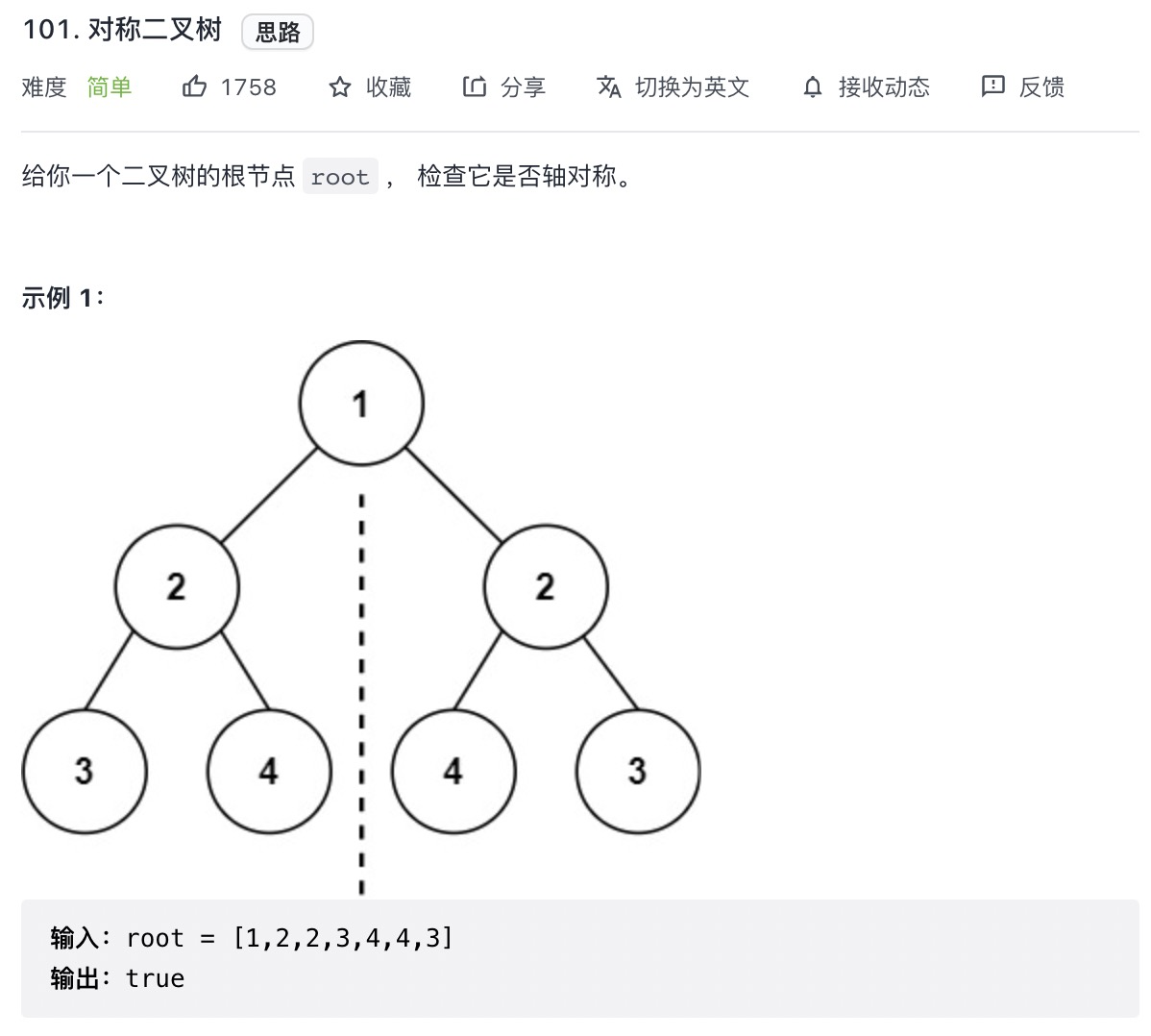
var isSymmetric = function(root) {
  /**
   * 思路：判断左右子树是否是镜像相等的，我们需要传入两个节点参数，首先左右子节点值是否相等，然后还要判断左右子节点的左子树和右子树是否相等，最后处理特殊情况
   *
   * 设传入的左右节点为left,right，依题意有以下情况
   * 1. left === null && right === null 对称
   * 2. left === null || right === null 非对称
   * 3. left.val === right.val && 递归函数(left.left,right.right) && 递归函数(left.right,right.left) 对称
   */
  if (!root) return true;
  let isEqual = (left, right) => {
    if (!left && !right) return true;
    if (!left || !right) return false;
    return left.val === right.val && isEqual(left.left, right.right) && isEqual(left.right, right.left);
  };
  return isEqual(root.left, root.right);
};

# 平衡二叉树 (opens new window)(高频 ❤️❤️❤️)

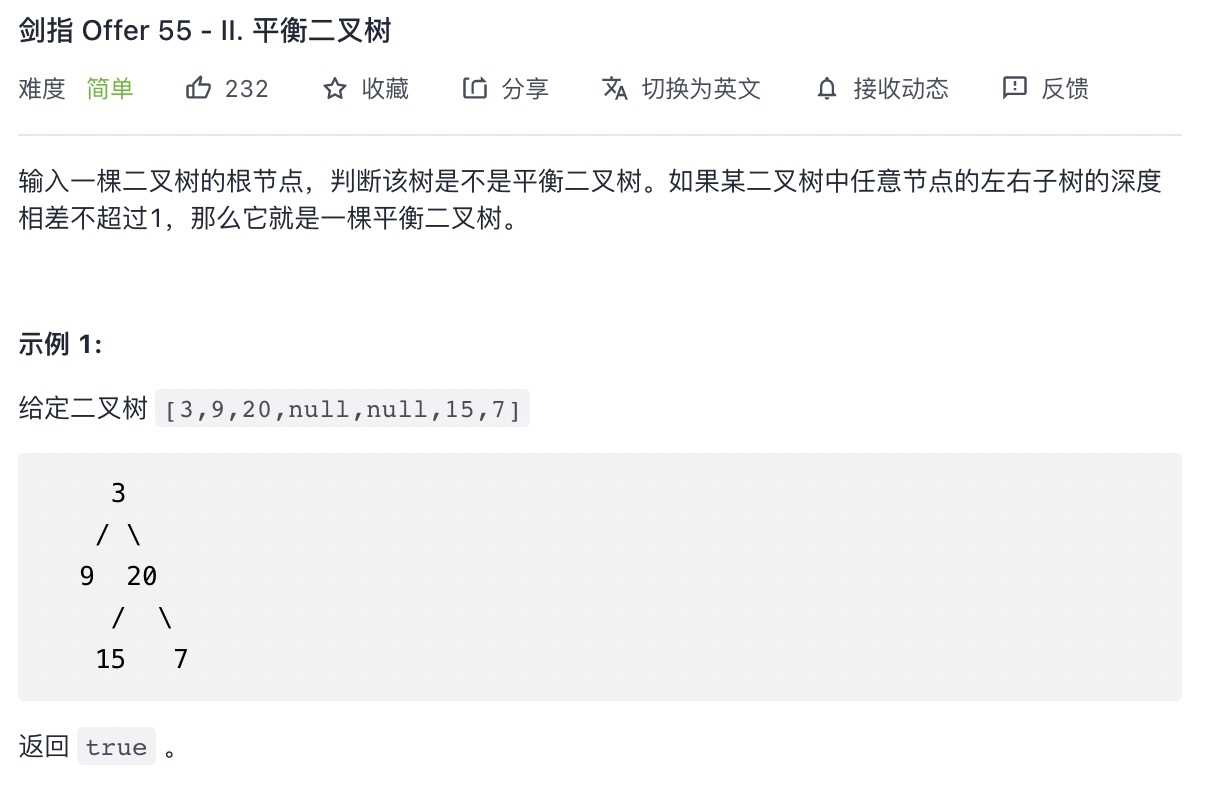
var isBalanced = function(root) {
  let treeDepth = root => {
    if (!root) {
      return 0;
    }
    return 1 + Math.max(treeDepth(root.left), treeDepth(root.right));
  };
  // 递归终止条件
  if (!root) return true;
  // 左子树为平衡二叉树并且右子树也为平衡二叉树 并且深度相差<=1
  return Math.abs(treeDepth(root.left) - treeDepth(root.right)) <= 1 && isBalanced(root.left) && isBalanced(root.right);
};

# 二叉树的镜像 (opens new window)

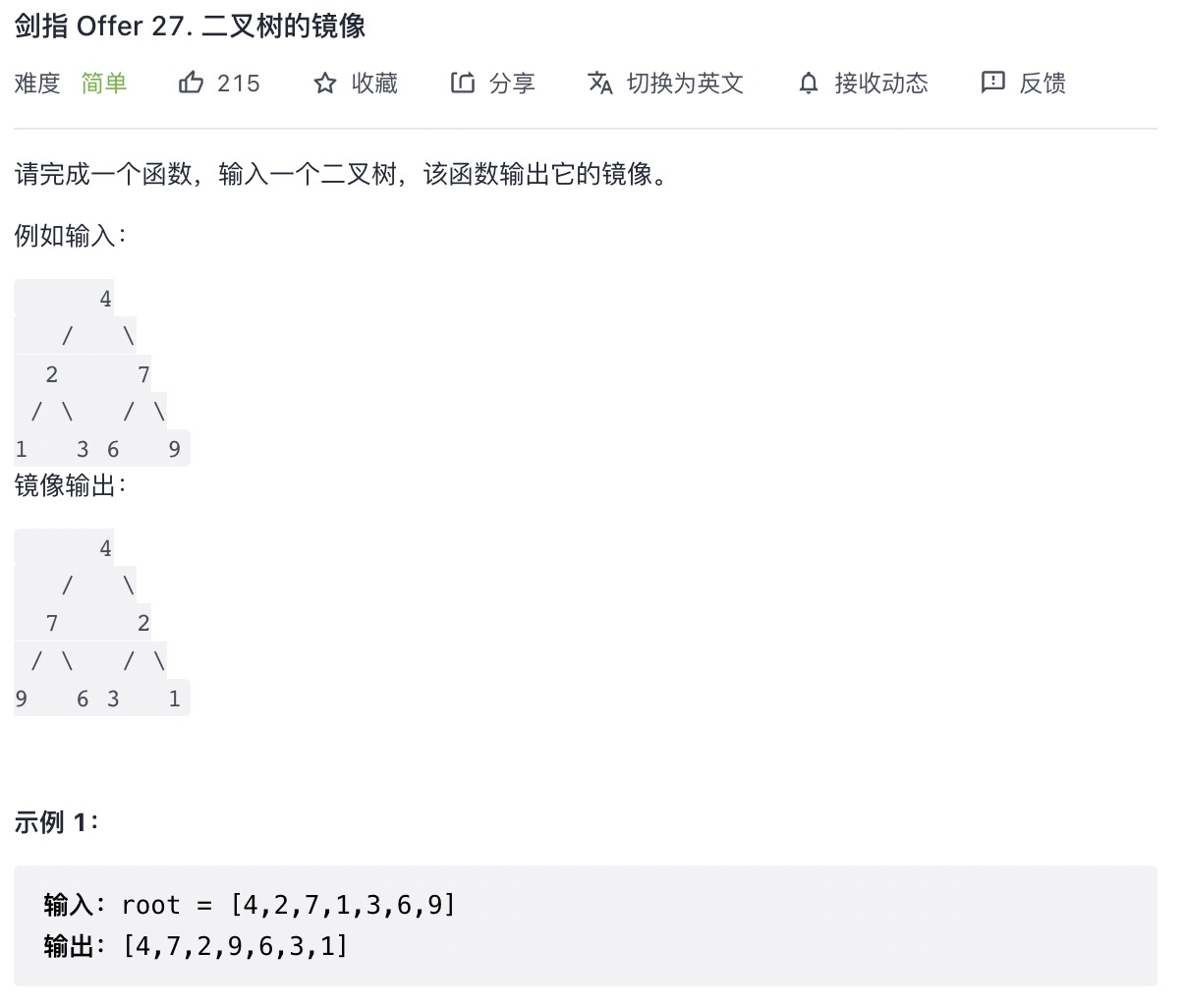
var mirrorTree = function(root) {
  /**
   * 思路：需要以数组形式拷贝左右子树 然后递归
   * */
  // null 返回本身
  if (!root) {
    return root;
  }
  // 左右数树，复制
  [root.left, root.right] = [root.right, root.left];
  mirrorTree(root.left);
  mirrorTree(root.right);
  return root;
};

# 验证二叉搜索树 (opens new window)(高频 ❤️❤️❤️)

var isValidBST = function(root) {
  var isValidBST = function(root) {
    /**
     * 思路：从一颗二叉树得出结论，可以给二叉树的值设置一个上下限值，
     * 满足二叉搜索树的左子树的上限就是根节点的值，
     * 满足二叉搜索树的右子树的下限就是根节点的值，
     * 然后递归即可
     */
    let helper = (node, lower, upper) => {
      if (!node) {
        return true;
      }
      // 节点的值保证在范围内
      if (node.val <= lower || node.val >= upper) {
        return false;
      }
      // 根节点处理完了，处理左右子树
      return helper(node.left, lower, node.val) && helper(node.right, node.val, upper);
    };
    // 初始化下限和上限
    return helper(root, -Infinity, Infinity);
  };
};

# 剑指 Offer 33. 二叉搜索树的后序遍历序列 (opens new window)

var verifyPostorder = function(postorder) {
  /**
   * 思路：通过后序遍历找到跟节点，然后划分左右子树，需要保证左节点小于根节点，右节点大于根节点，最后递归传入后序遍历树的左右子树判断
   */
  let len = postorder.length;
  // 只有一个或者没有结点
  if (len < 2) return true;

  // root
  let root = postorder[len - 1];
  // 划分左右,假设i就是分界点
  let i = 0;
  for (; i < len - 1; i++) {
    // 左子树需要小于跟
    if (postorder[i] > root) {
      break;
    }
  }
  // 拿到右子树,保证右子树每个都大于root
  let result = postorder.slice(i, len - 1).every(item => item > root);
  // 如果满足二叉搜索树,继续递归后序的左右子树
  if (result) {
    return verifyPostorder(postorder.slice(0, i)) && verifyPostorder(postorder.slice(i, len - 1));
  } else {
    return false;
  }
};

# 把二叉搜索树转换为累加树 (opens new window)

var convertBST = function(root) {
  /**
     * 思路：二叉搜索树的中序遍历必定是一个升序的数组，这里借助到反向中序遍历实现
      1.定义一个全局变量sum，用于存储遍历的所有节点值的累计和；
      2.递归终止条件： root为空就返回null;
      3.递归右子树root.right;
      4.遍历当前节点，作如下操作：
         将其值累加到sum中；
         把sum赋值给当前节点的值；
      5.递归左子树root.left;
     */
  let sum = 0;
  let sumTree = root => {
    if (!root) {
      return null;
    }
    // 遍历右子树
    sumTree(root.right);
    // 计算sum和赋值
    sum += root.val;
    root.val = sum;
    // 遍历左子树
    sumTree(root.left);
    return root;
  };
  return sumTree(root);
};

# 将有序数组转换为二叉搜索树 (opens new window)

var sortedArrayToBST = function(nums) {
  /**
   * 思路：将数组才分为左根右，然后递归构建树
   */
  let length = nums.length;
  if (!length) return null;
  let mid = Math.floor(length / 2);
  // 根节点
  let root = new TreeNode(nums[mid]);
  // 递归构建
  root.left = sortedArrayToBST(nums.slice(0, mid));
  root.right = sortedArrayToBST(nums.slice(mid + 1, length));
  return root;
};

# 有序链表转换二叉搜索树 (opens new window)

var sortedListToBST = function(head) {
  var stack = [];
  while (head) {
    stack.push(head.val);
    head = head.next;
  }
  function transformTree(nums) {
    if (!nums.length) return null;
    const mid = Math.floor(nums.length / 2);
    let root = new TreeNode(nums[mid]);
    root.left = transformTree(nums.slice(0, mid));
    root.right = transformTree(nums.slice(mid + 1));
    return root;
  }
  return transformTree(stack);
};

# (高频 ❤️❤️❤️)从前序与中序遍历序列构造二叉树 (opens new window)

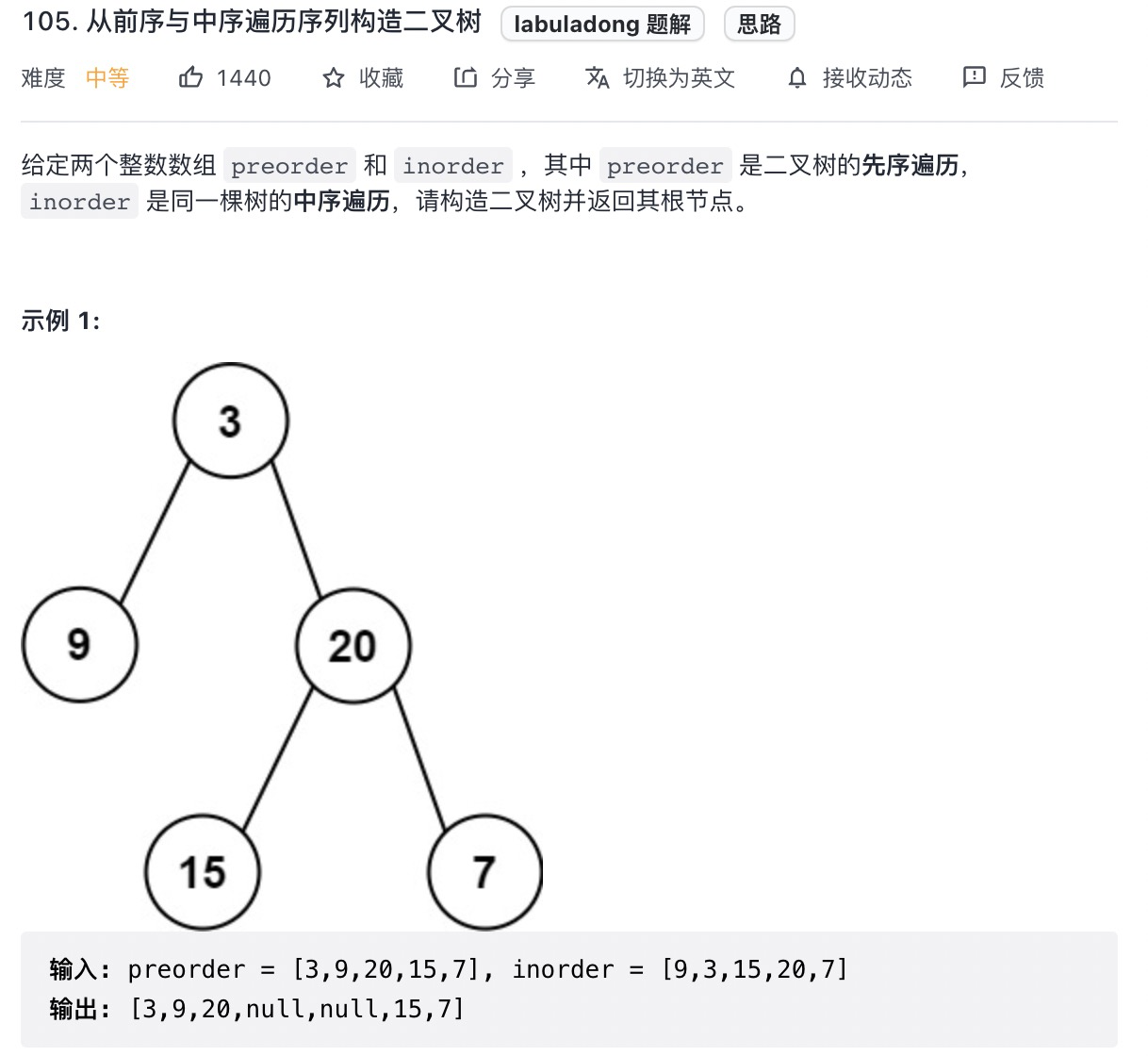
var buildTree = function(preorder, inorder) {
  /**
   * 递归结束条件 ：二者都不为空 否则返回null
   * 思路：前序遍历第一个节点一定是跟节点，然后确定根节点在中序遍历的位置，用key记录，然后前序的左子树和中序的左子树继续递归
   * 1. root.left 就等于前序遍历的左子树和中序遍历的左子树递归
   * root.left = buildTree(preorder.slice(1,key+1),inorder.slice(0,key))
   * 2. root.right 就等于前序遍历的右子树和中序遍历的右子树递归
   * root.right = buildTree(preorder.slice(key+1),inorder.slice(key+1))
   * 最后返回root
   */
  if (!preorder.length || !inorder.length) {
    return null;
  }
  let key = 0;
  // 构建树
  let root = new TreeNode(preorder[0]);
  // 找到根节点在中序的位置
  for (let i = 0; i < inorder.length; i++) {
    if (inorder[i] === preorder[0]) {
      key = i;
    }
  }
  // 左右子树通过递归构建
  root.left = buildTree(preorder.slice(1, key + 1), inorder.slice(0, key));
  root.right = buildTree(preorder.slice(key + 1), inorder.slice(key + 1));
  return root;
};

# 合并二叉树 (opens new window)

var mergeTrees = function(t1, t2) {
  /**
   * 思路：dfs 假设累加和的树根节点为t1,t1节点的值等于t2累加，最后返回t1或者t2
   * t1.val+=t2.val
   * t1.left = mergeTrees(t1.left,t2.left)
   * t1.right = mergeTrees(t1.right,t2.right)
   */

  // 保证t1和t2有值
  if (t1 && t2) {
    t1.val += t2.val;
    t1.left = mergeTrees(t1.left, t2.left);
    t1.right = mergeTrees(t1.right, t2.right);
  }
  return t1 || t2; // 返回有值的即可
};

# 树的子结构 (opens new window)

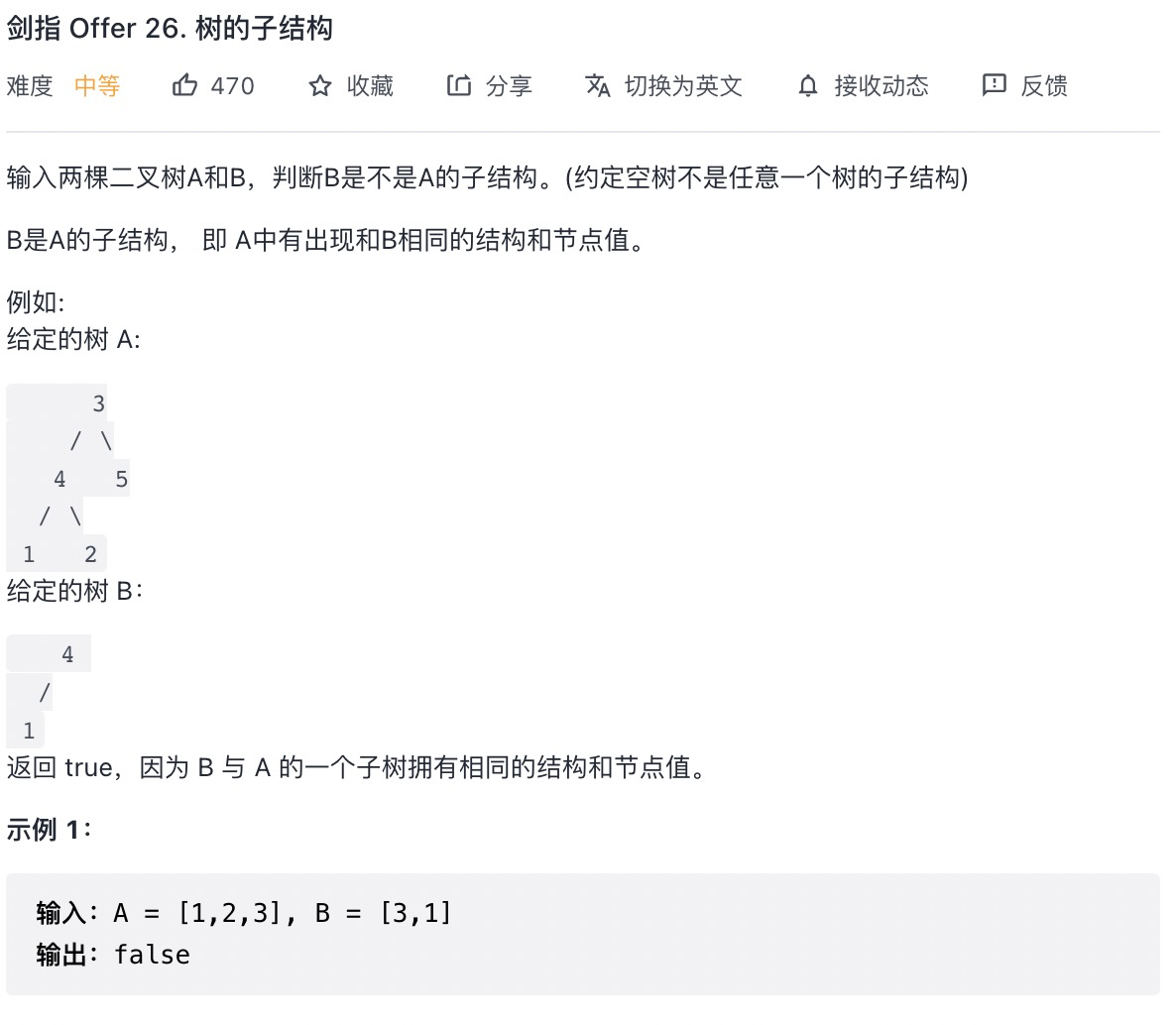
var isSubStructure = function(A, B) {
  /**
   * 思路：
   * 1. 判断子结构过程：判断A,B节点是否相等，不相等则直接返回false，否则继续判断左右子节点是否相等
   * 2. B可能是A根节点的子结构，也可能是左右子树的子结构
   * 3. 递归终止条件：两棵树有一颗不存在，返回false，判断子结构时，B为空树返回true，A为空树返回false
   */
  // 判断root2是否是root1的子结构
  function isSubtree(root1, root2) {
    if (!root2) return true;
    if (!root1) return false;
    if (root1.val !== root2.val) return false;
    return isSubtree(root1.left, root2.left) && isSubtree(root1.right, root2.right);
  }
  // 递归终止条件
  if (!A || !B) {
    return false;
  }
  // 这里一定要写清楚函数，跟节点是否为subTree 左右子树是否为subTree调用的函数不一样
  return isSubtree(A, B) || isSubStructure(A.left, B) || isSubStructure(A.right, B);
};

# 相同的树 (opens new window)

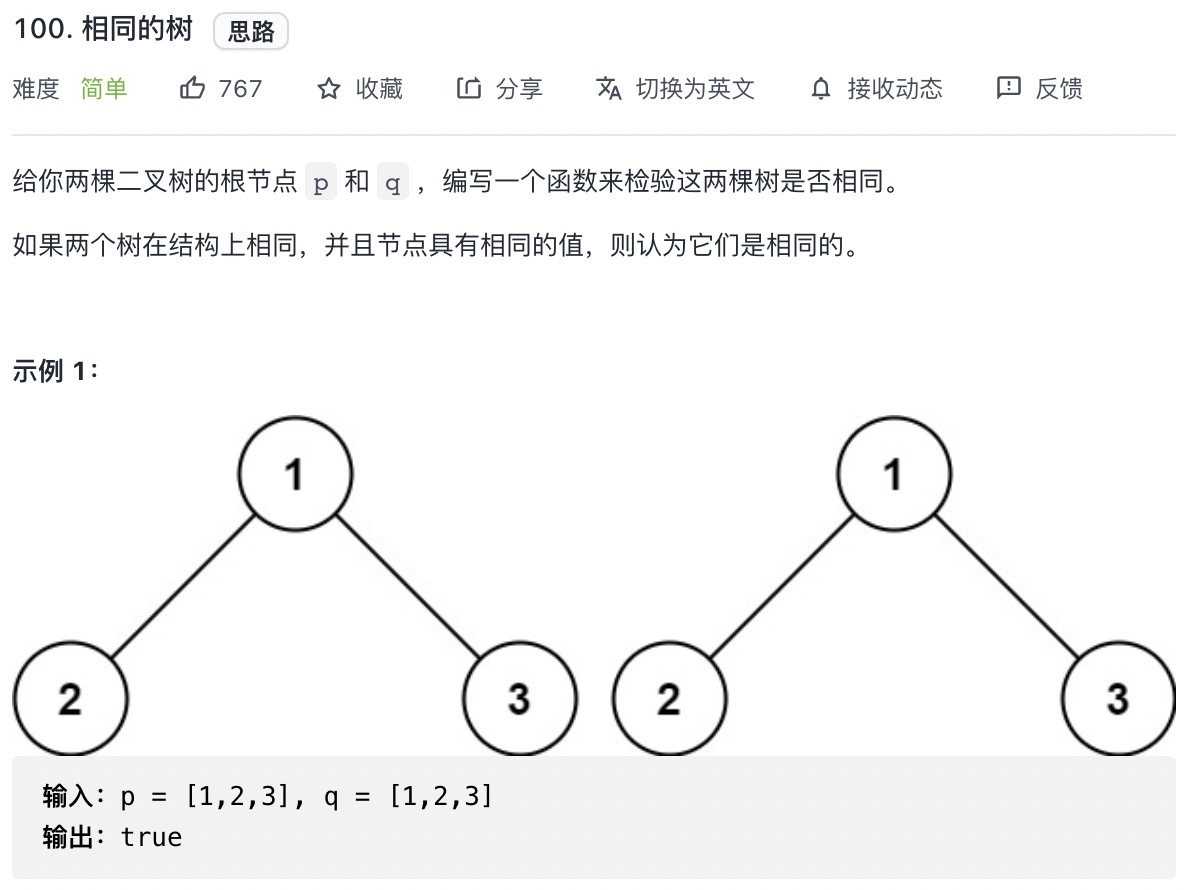
var isSameTree = function(p, q) {
  /**
   * 思路：先判断根节点 再递归判断左右子树，记得带上递归终止条件 思路类似判断树的子结构
   */
  // 递归终止条件
  if (!p && !q) return true;
  if (!p && q) return false;
  if (p && !q) return false;
  // 首先判断根
  if (p.val !== q.val) return false;
  // 左右子树
  if (isSameTree(p.left, q.left) && isSameTree(p.right, q.right)) {
    return true;
  } else {
    return false;
  }
};

# 求二叉树的路径

# 路径总和 (opens new window)(高频 ❤️❤️❤️)

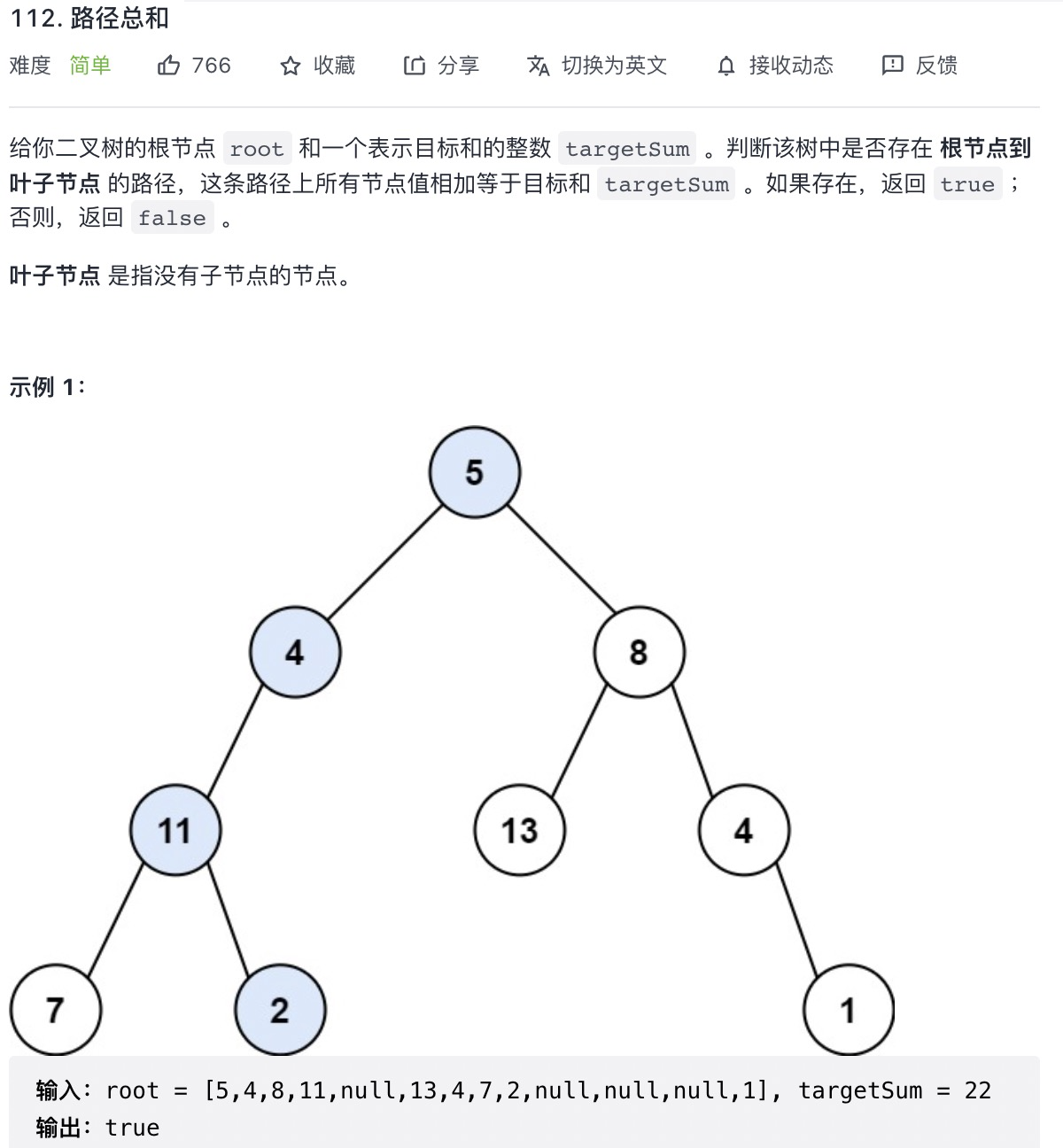
var hasPathSum = function(root, sum) {
  /**
   * 思路：使用dfs遍历，累加每个节点的和，当到达底部系欸但时，判断是否发满足条件即可
   */
  if (!root) {
    return false;
  }
  let res = false;
  let dfs = (root, s) => {
    if (!root.left && !root.right && s === sum) {
      res = true;
    }
    if (root.left) {
      dfs(root.left, s + root.left.val);
    }
    if (root.right) {
      dfs(root.right, s + root.right.val);
    }
  };
  dfs(root, root.val);
  return res;
};

# 求二叉树的所有路径 (opens new window)

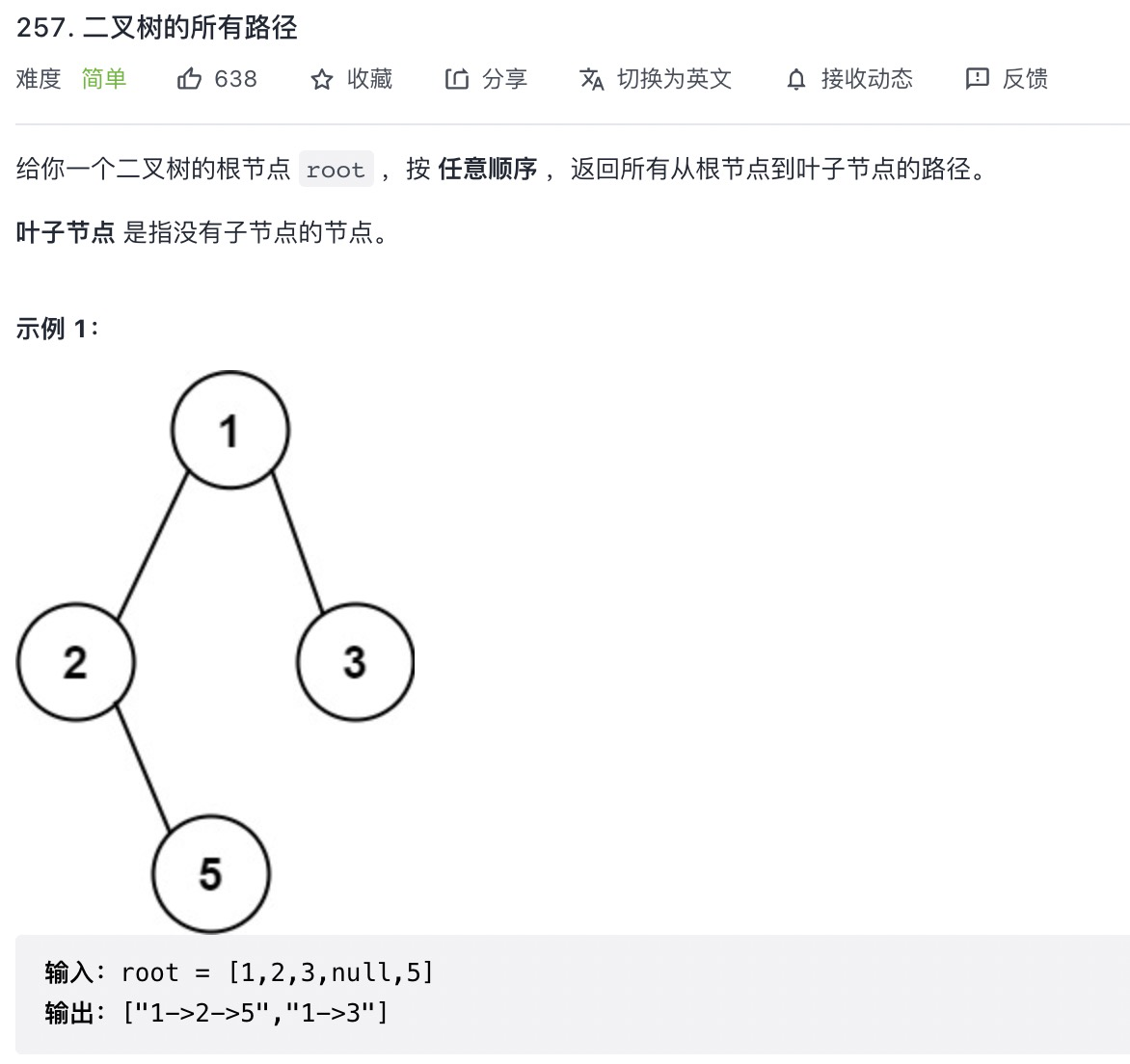
const binaryTreePaths = root => {
  const res = [];

  const buildPath = (root, pathStr) => {
    if (root == null) {
      // 遍历到null
      return; // 结束当前递归分支
    }
    if (root.left == null && root.right == null) {
      // 遍历到叶子节点
      pathStr += root.val; // 路径末尾了，不用加箭头
      res.push(pathStr); // 加入解集
      return;
    }
    pathStr += root.val + "->"; // 处理非叶子节点，要加箭头
    buildPath(root.left, pathStr); // 基于当前的pathStr，递归左子树
    buildPath(root.right, pathStr); // 基于当前的pathStr，递归右子树
  };

  buildPath(root, "");
  return res;
};

# 求根到叶子节点数字之和 (opens new window)(高频 ❤️❤️❤️)

var sumNumbers = function(root) {
  /**
   * 将每个节点代表的数字当作字符串，然后使用dfs便利拼接，最后累加起来
   */

  let res = 0;
  let dfs = (root, num) => {
    if (!root) {
      return;
    }
    // 当作字符串拼接，就不需要管十位还是个位了
    num += root.val;
    if (!root.left && !root.right) {
      res += Number(num);
    }
    dfs(root.left, num);
    dfs(root.right, num);
  };
  dfs(root, "");
  return res;
};

# 路径总和|| (opens new window)(高频 ❤️❤️❤️)

var pathSum = function(root, sum) {
  /**
   * 思路：回溯算法：
   * 1. 路径：等于sum的节点数组
   * 2. 选择列表: 所有的节点
   * 3. 终止条件：node等于null
   */
  // 结果集 当前路径
  let res = [],
    stack = [];
  // 使用dfs完成
  let dfs = (node, sum) => {
    // 终止条件
    if (!node) return;
    // 做选择
    sum -= node.val;
    stack.push(node.val);
    // 如果sum = 0，并且无左右子树,将路径保存在结果集
    if (sum === 0 && !node.left && !node.right) {
      res.push([...stack]);
    }
    // 递归
    node.left && dfs(node.left, sum);
    node.right && dfs(node.right, sum);
    // 撤销选择
    stack.pop();
  };
  dfs(root, sum);
  return res;
};

# 路径总和 III (opens new window)(高频 ❤️❤️❤️)

/**
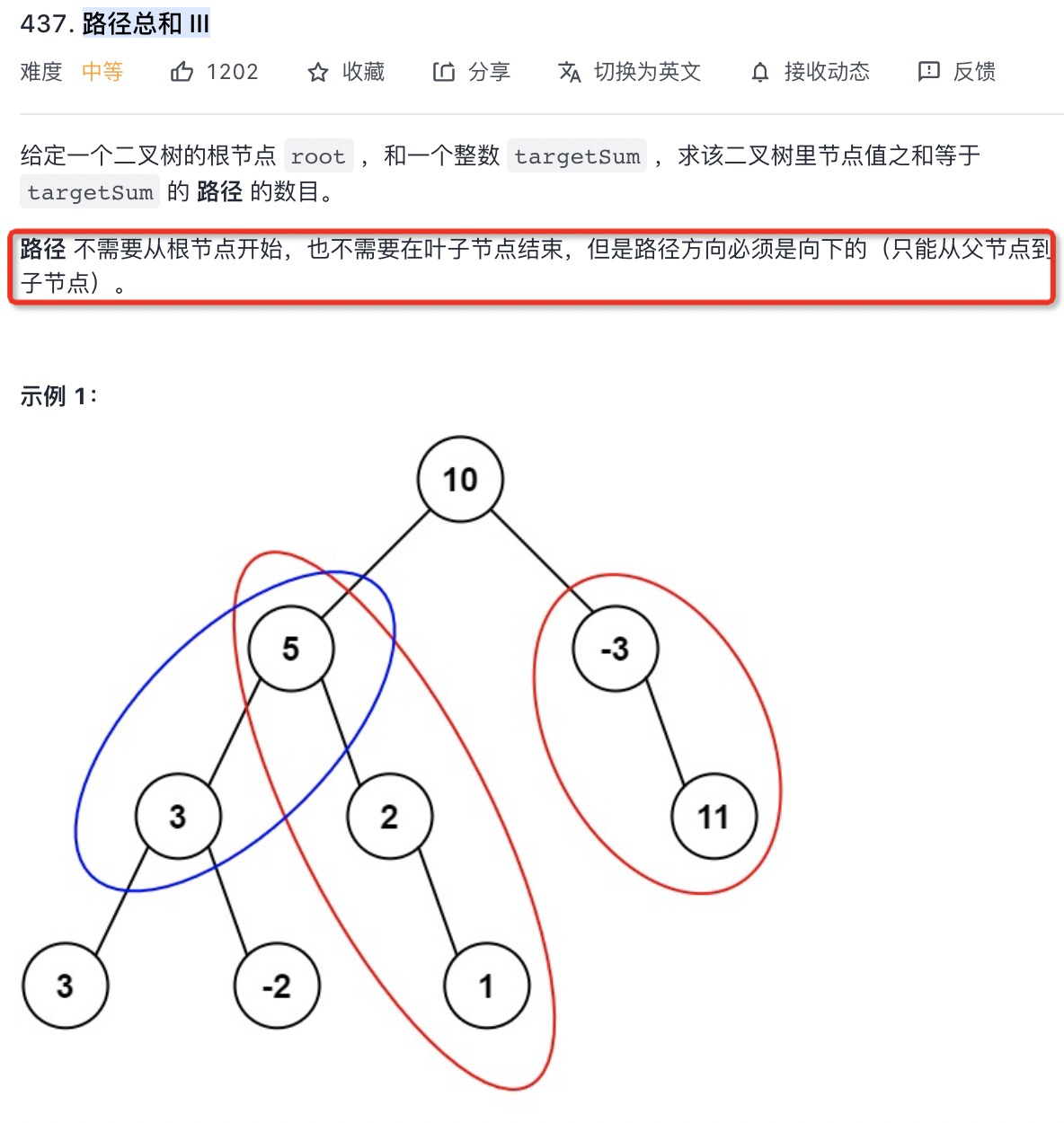
 * @param {TreeNode} root
 * @param {number} targetSum
 * @return {number}
 */
var pathSum = function(root, targetSum) {
  let res = 0;

  if (!root) {
    return 0;
  }
  function backTrack(node, sum) {
    if (!node) {
      return;
    }
    sum -= node.val;
    if (sum === 0) {
      res++;
    }
    // 递归
    if (node.left) {
      backTrack(node.left, sum);
    }
    if (node.right) {
      backTrack(node.right, sum);
    }
  }
  backTrack(root, targetSum);
  // 因为路径不需要从根节点开始，也不需要在叶子节点结束，所以要分别从左右树出发计算路线
  res += pathSum(root.left, targetSum);
  res += pathSum(root.right, targetSum);

  return res;
};

# 其他

# 二叉树展开为链表 (opens new window)(高频 ❤️❤️❤️)

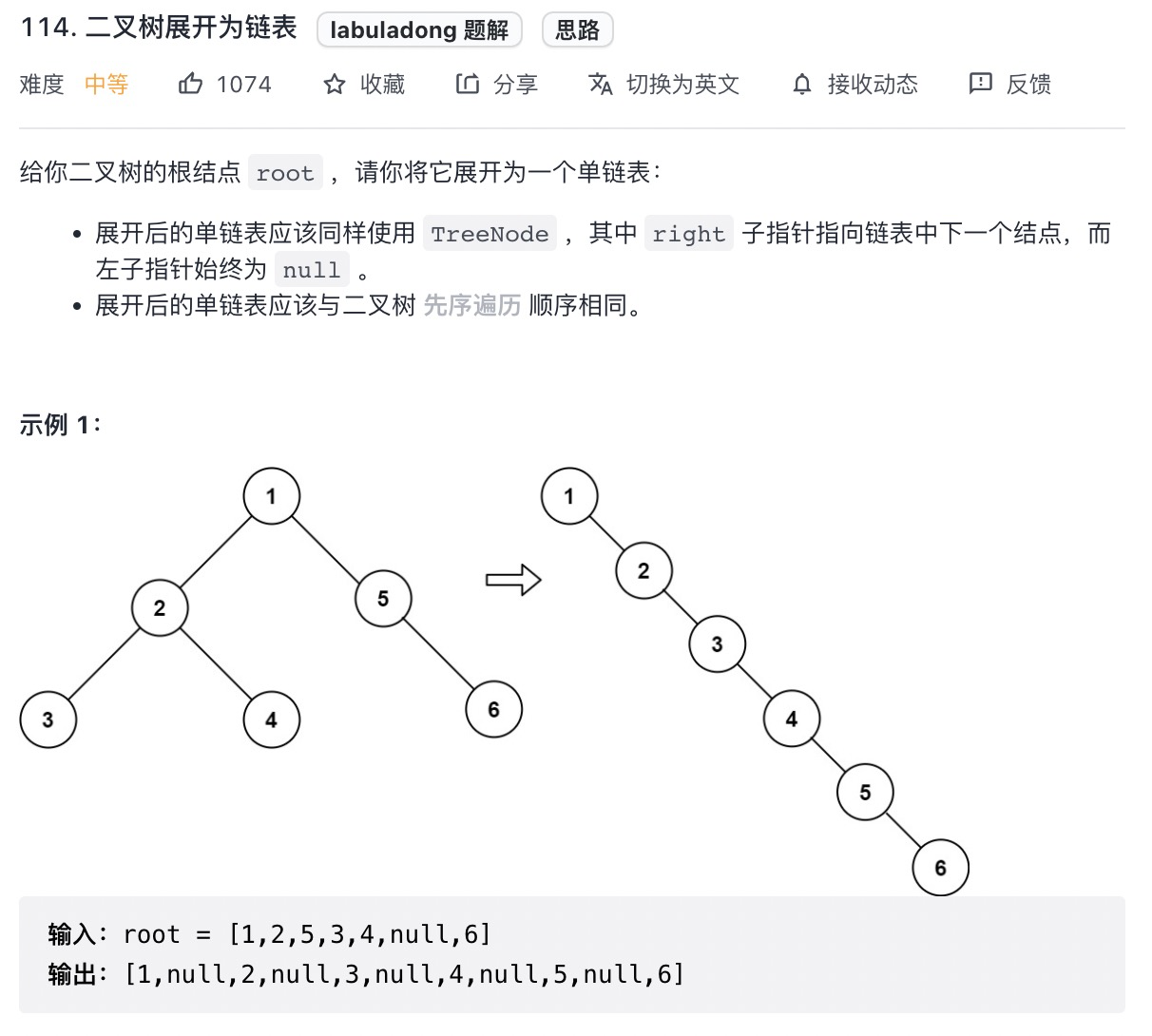
思路：

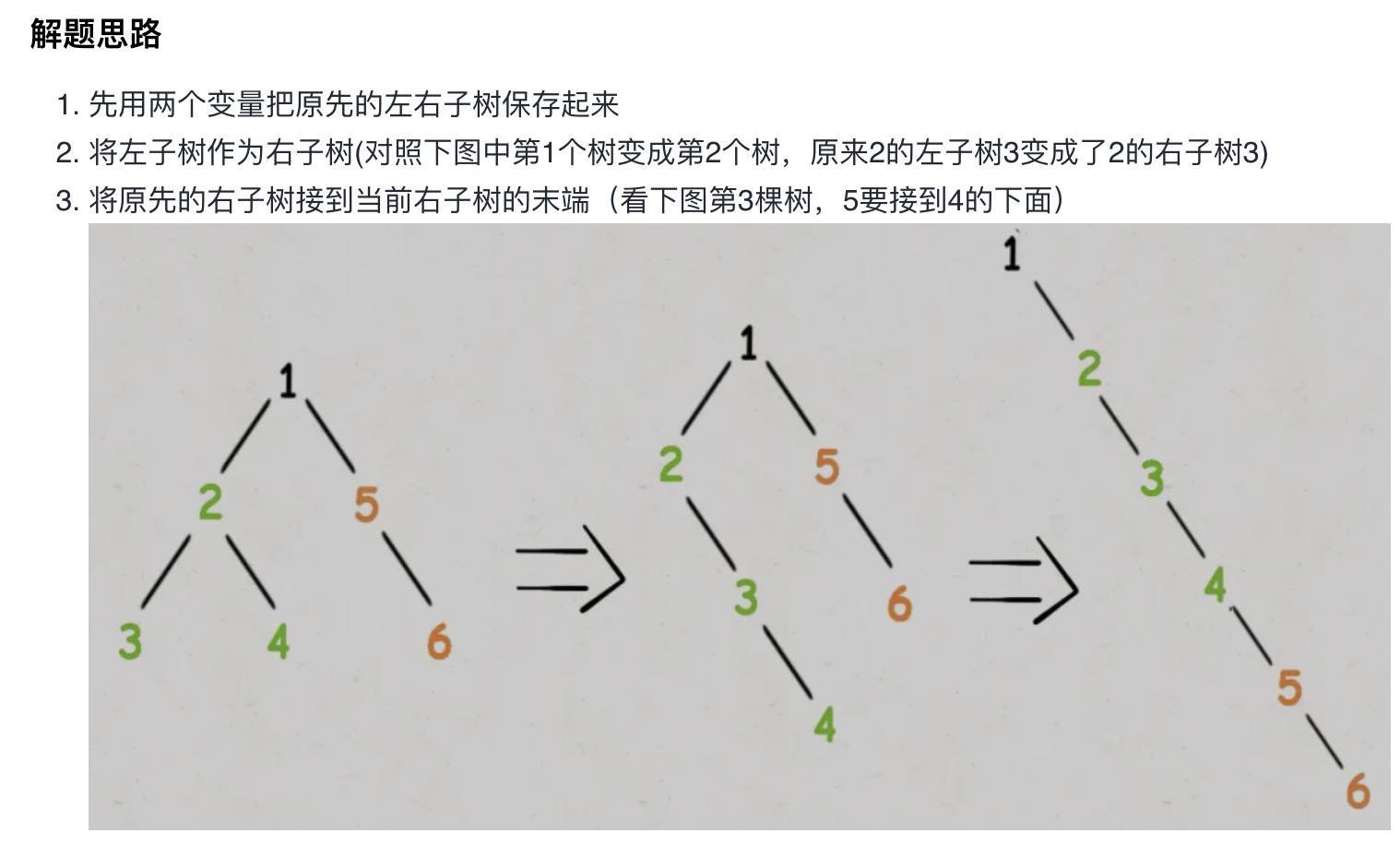
var flatten = function(root) {
  /**
   * 1. 将左右子树打平，这一步其实就是在调用递归
   * 2. 将根节点的右子树 接在 根节点的左子树打平后的最右边节点上的右子树上，
   * 3. 最后需要将整棵二叉树的左子树置空，右子树更新为拼接好的树
   */
  let dfs = root => {
    if (!root) {
      return;
    }
    // 将左右子树拉平
    dfs(root.left);
    dfs(root.right);
    let pre = root.left;
    if (pre) {
      // 获取根节点下左子树的最右节点:pre
      while (pre.right) {
        pre = pre.right;
      }
      // 最右节点右子树连接根节点的右子树
      pre.right = root.right;
      // 将整棵树的右子树的值设为左子树的值，然后置空左子树
      root.right = root.left;
      root.left = null;
    }
  };
  dfs(root);
  return root;
};

# 填充每个节点的下一个右侧节点指针 (opens new window)

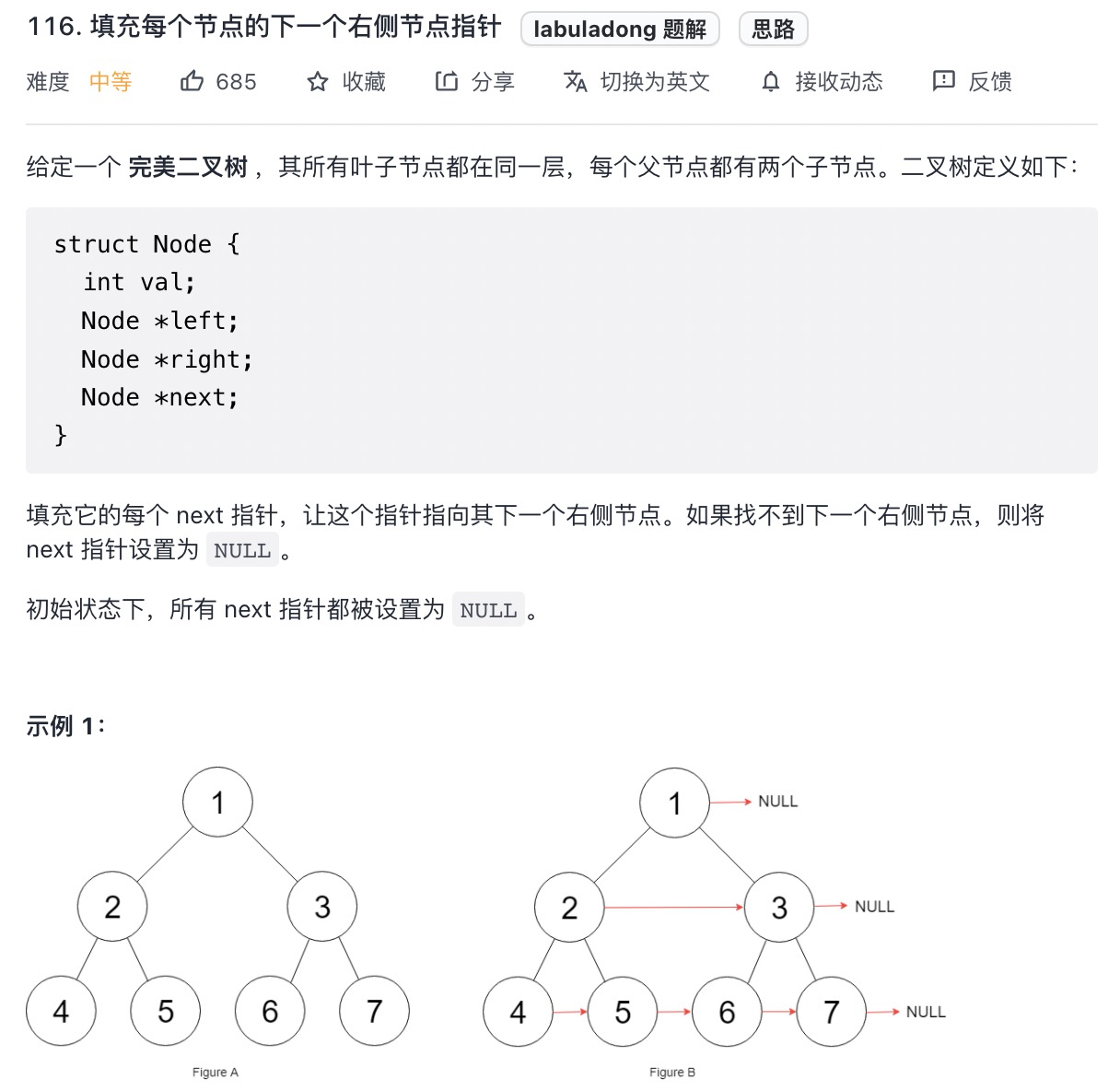
var connect = function(root) {
  /**
   * 1. node1 和 node2 需要连接在一起
   * 2. 考虑将同一父节点的左右子树需要连接在一起
   * 3. 不同父节点的左右子树需要连接在一起 node1.right = node2.left
   */
  function changePosition(node1, node2) {
    // 传入的节点不能为空
    if (node1 === null || node2 === null) {
      return;
    }
    // 连接
    node1.next = node2;
    // 自己的
    changePosition(node1.left, node1.right);
    changePosition(node2.left, node2.right);
    // 不同父的
    changePosition(node1.right, node2.left);
  }
  if (!root) {
    return null;
  }
  changePosition(root.left, root.right);
  return root;
};

# 堆

# 数组中的第 K 个最大元素 (opens new window)(高频 ❤️❤️❤️)

class MiniHeap {
  constructor() {
    // 定义堆
    this.heap = [];
  }
  // 千万不要写成m和n交换
  swap(m, n) {
    let temp = this.heap[m];
    this.heap[m] = this.heap[n];
    this.heap[n] = temp;
  }
  /**
   * 插入: 插入元素到底部，然后将该元素做上移操作(需要满足父节点必须小于等于子节点)
   * @param {*} value 插入元素值
   */
  insert(value) {
    this.heap.push(value);
    this.shiftUp(this.heap.length - 1);
  }
  // 上移，比较父节点和子节点的大小,如果不符合条件就交换元素，然后对新的元素继续进行上移操作
  shiftUp(index) {
    // 堆顶不上移
    if (index === 0) {
      return;
    }
    const parentIndex = Math.floor(index - 1 / 2);
    if (this.heap[parentIndex] > this.heap[index]) {
      this.swap(parentIndex, index);
      this.shiftUp(parentIndex);
    }
  }
  // 堆大小
  len() {
    return this.heap.length;
  }
  /**
   * 删除: 不能直接删除堆顶元素，需要用数组尾元素替换堆顶元素，然后进行下移操作
   */
  pop() {
    // 替换堆顶元素先
    this.heap[0] = this.heap.pop();
    // 下移
    this.shiftDown(0);
  }
  // 下移操作，这里我们需要保证子节点是大于等于父节点的
  shiftDown(index) {
    const leftChildIndex = 2 * index + 1;
    const rightChildIndex = 2 * index + 2;
    if (this.heap[index] > this.heap[leftChildIndex]) {
      this.swap(index, leftChildIndex);
      this.shiftDown(leftChildIndex);
    }
    if (this.heap[index] > this.heap[rightChildIndex]) {
      this.swap(index, rightChildIndex);
      this.shiftDown(rightChildIndex);
    }
  }
  // 获取堆顶元素
  heep() {
    return this.heap[0];
  }
}
var findKthLargest = function(nums, k) {
  /**
   * 思路：最小堆或者直接使用排序
   */
  // let h1 = new MiniHeap()
  // nums.forEach(num=>{
  //     h1.insert(num)
  //     if(h1.len() > k){
  //         h1.pop()
  //     }
  // })
  // return h1.heep()
  nums = nums.sort((a, b) => b - a);
  return nums[k - 1];
};

# 前 K 个高频元素 (opens new window)(高频 ❤️❤️❤️)

class MinHeep {
  constructor() {
    this.heep = [];
  }
  swap(m, n) {
    let temp = this.heep[m];
    this.heep[m] = this.heep[n];
    this.heep[n] = temp;
  }
  shiftUp(index) {
    if (index === 0) {
      return;
    }
    let parentIndex = Math.floor(index - 1 / 2);
    // 可能会取到undefined
    if (this.heep[parentIndex].value && this.heep[parentIndex].value > this.heep[index].value) {
      this.swap(parentIndex, index);
      this.shiftUp(parentIndex);
    }
  }
  shifDown(index) {
    let leftChildIndex = 2 * index + 1;
    let rightChildIndex = 2 * index + 2;
    // 可能会取到undefined
    if (this.heep[leftChildIndex] && this.heep[leftChildIndex].value < this.heep[index].value) {
      this.swap(leftChildIndex, index);
      this.shifDown(leftChildIndex);
    }
    if (this.heep[rightChildIndex] && this.heep[rightChildIndex].value < this.heep[index].value) {
      this.swap(rightChildIndex, index);
      this.shifDown(rightChildIndex);
    }
  }
  insert(value) {
    this.heep.push(value);
    this.shiftUp(this.heep.length - 1);
  }
  delete() {
    this.heep[0] = this.heep.pop();
    this.shifDown(0);
  }
  top() {
    return this.heep[0];
  }
}
var topKFrequent = function(nums, k) {
  /**
   * 按照题意有两种解法：
   * 1. 用map保存每个数出现的次数为value，数为key，然后将map转为数组进行排序，最后截取前k个元素即可，时间复杂度：O(nlogn),不符合题意
   * 2. 用map保存每个数出现的次数为value，数为key，然后使用最小堆将{key,value}对象插入，这时需要改造下最小堆的类。当容积大于k时，移除堆顶元素，最后返回堆的key组成的数组即可
   */

  // 最优做法
  // 首先使用map记录各个元素出现的次数
  let map = new Map();
  nums.forEach(num => {
    map.set(num, map.has(num) ? map.get(num) + 1 : 1);
  });
  // // 使用最小堆解决问题
  // let h1 = new MinHeep()
  // // 记住这里是value-key
  // map.forEach((value,key)=>{
  //     h1.insert({value,key})
  //     // 如果超过k
  //     if(h1.heep.length > k){
  //         h1.delete()
  //     }
  // })
  // return h1.heep.map(obj=>obj.key)

  // 使用排序O(nlogn)
  let sortMapArray = Array.from(map).sort((a, b) => b[1] - a[1]);
  return sortMapArray.map(arr => arr[0]).slice(0, k);
};

# 二分查找

# 二分查找 (opens new window)(高频 ❤️❤️❤️)

var search = function(nums, target) {
  let low = 0;
  let high = nums.length - 1;
  while (low <= high) {
    let mid = Math.floor((low + high) / 2);
    let Element = nums[mid];
    if (Element === target) {
      return mid;
    } else if (Element > target) {
      high = mid - 1;
    } else if (Element < target) {
      low = mid + 1;
    }
  }
  return -1;
};

# 在排序数组中查找元素的第一个和最后一个位置 (opens new window)(高频 ❤️❤️❤️)

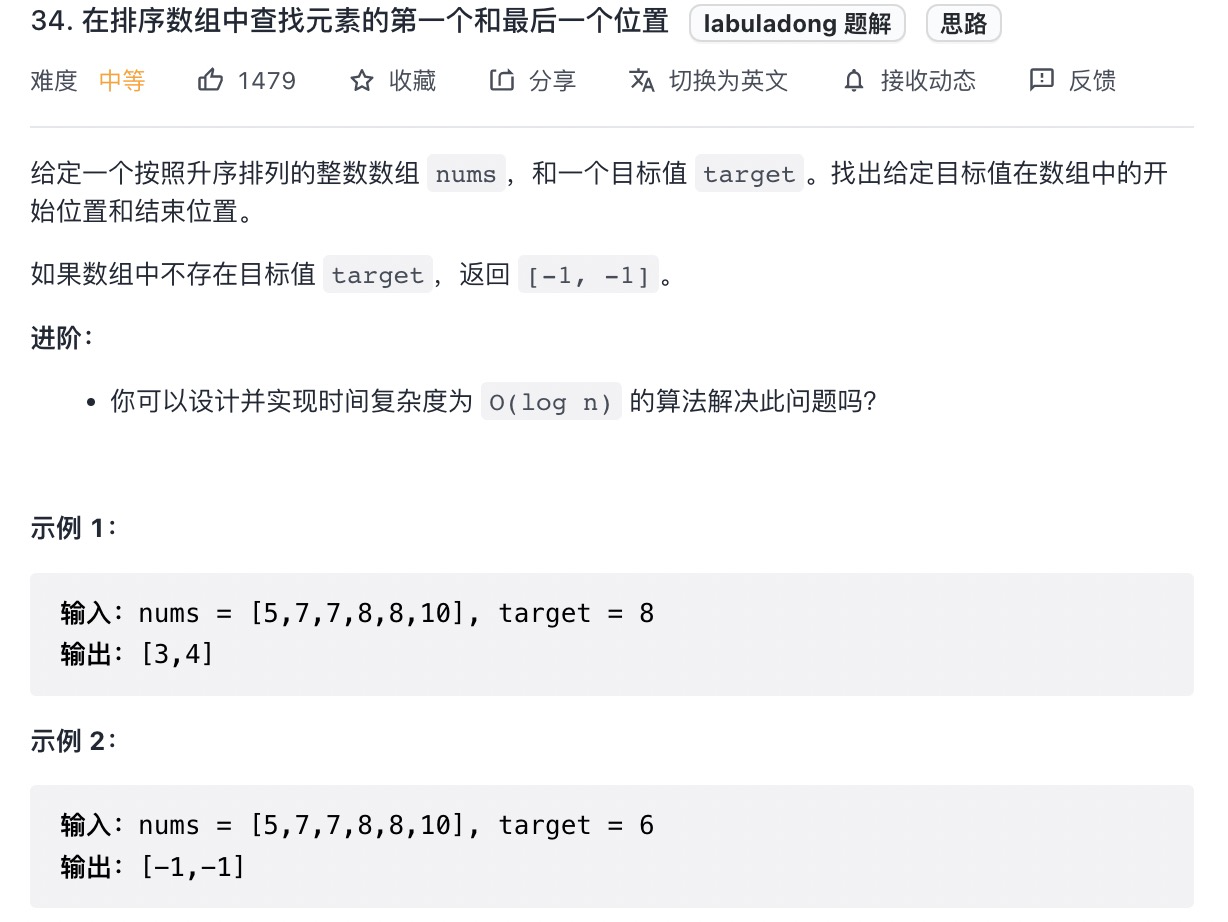
不要花里胡哨，分开求

var searchRange = function(nums, target) {
  return [getLeftBoundary(), getRightBoundary()];
  function getLeftBoundary() {
    let left = 0;
    let right = nums.length - 1;
    while (left <= right) {
      let mid = Math.floor((left + right) / 2);
      let element = nums[mid];
      if (element > target) {
        right = mid - 1;
      } else if (element < target) {
        left = mid + 1;
      } else {
        right = mid - 1;
      }
    }
    if (left >= nums.length || nums[left] !== target) {
      return -1;
    }
    return left;
  }
  function getRightBoundary() {
    let left = 0;
    let right = nums.length - 1;
    while (left <= right) {
      let mid = Math.floor((left + right) / 2);
      let element = nums[mid];
      if (element > target) {
        right = mid - 1;
      } else if (element < target) {
        left = mid + 1;
      } else {
        left = mid + 1;
      }
    }
    if (right < 0 || nums[right] !== target) {
      return -1;
    }
    return right;
  }
};

# 0 ～ n-1 中缺失的数字 (opens new window)(高频 ❤️❤️❤️)

var missingNumber = function(nums) {
  let left = 0;
  let right = nums.length - 1;
  while (left <= right) {
    const mid = Math.floor((left + right) / 2);
    // 0到mid中不存在，需要扩大左边界
    if (nums[mid] === mid) {
      left = mid + 1;
    } else {
      right = mid - 1;
    }
  }
  return left;
};

# x 的平方根 (opens new window)(高频 ❤️❤️❤️)

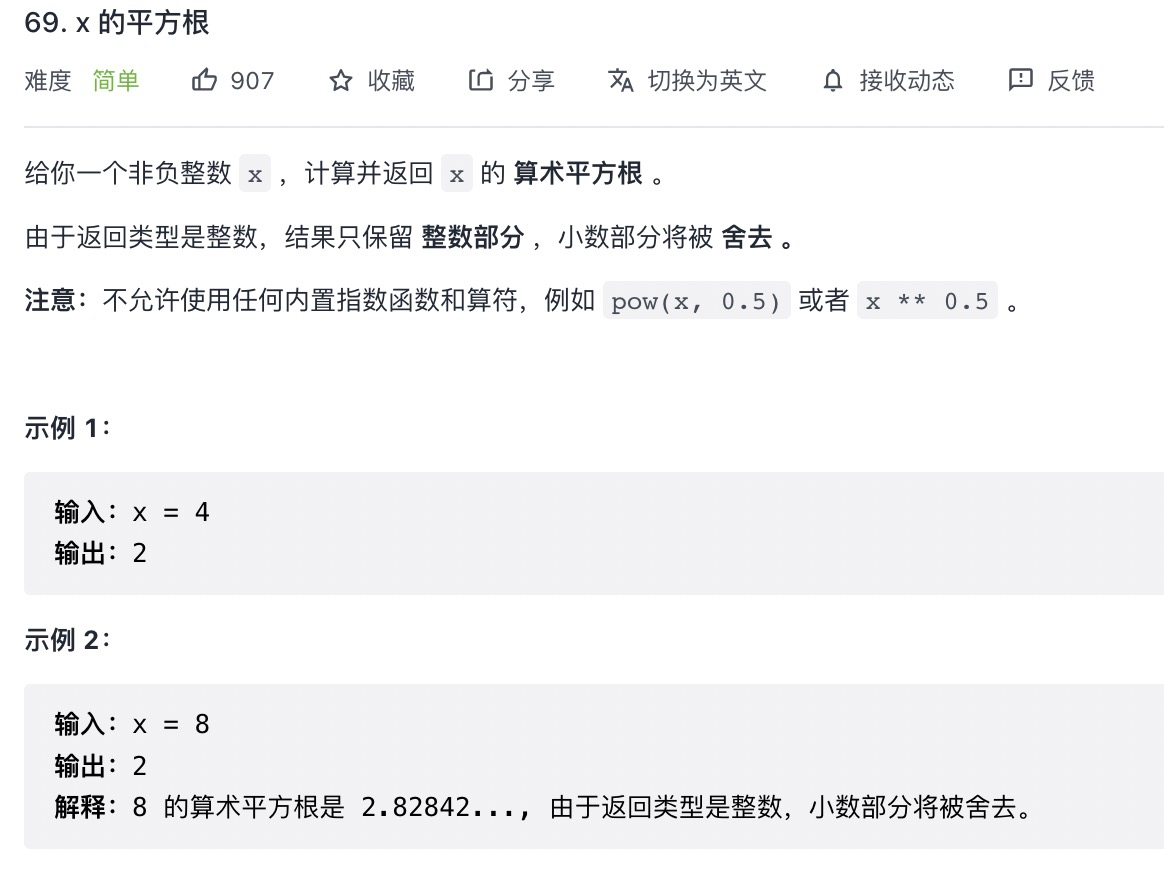
var mySqrt = function(x) {
  // 和二分法唯一的区别是 需要用res保存mid结果
  let left = 0;
  let right = x;
  let res;
  while (left <= right) {
    const mid = Math.floor((left + right) / 2);
    // 关键步骤一定要写对
    if (mid * mid <= x) {
      res = mid;
      left = mid + 1;
    } else {
      right = mid - 1;
    }
  }
  return res;
};

# Pow(x, n) (opens new window)

var myPow = function(x, n) {
  // pow(2,10) = pow(4,5) = 4 * pow(4, 4) = 4 * 16 * pow(16, 2) = 4 * 16 * 256 * pow(1, 1)
  // n为偶数 myPow(x*x,n/2)
  // n为奇数 x * myPow(x,n-1)
  if (n === 0) {
    return 1;
  }
  // 负数幂 幂倒
  if (n < 0) {
    n = -n;
    x = 1 / x;
  }
  if (n % 2 === 0) {
    return myPow(x * x, n / 2);
  } else return x * myPow(x, n - 1);
};

# 寻找旋转排序数组中的最小值 (opens new window)(高频 ❤️❤️❤️)

// 容易想到二分查找
// 在循环中求出 中间元素，循环条件是 left < right，结束遍历时，我们让left和right是相邻的整数，并且我们让left是我们要的
// 如果 nums[mid] > nums[right] ，则说明 mid 处在左边的单增区间，目标元素在mid的右侧，所以我们让 left = mid + 1;
// 否则，mid 处在右边的单增区间中，目标元素在mid的左侧，我们让right = mid;
// 一个+1，一个不+1，到时候取 left 就好
const findMin = nums => {
  let left = 0;
  let right = nums.length - 1;
  while (left < right) {
    const mid = left + ((right - left) >>> 1);
    if (nums[mid] > nums[right]) {
      left = mid + 1;
    } else {
      right = mid;
    }
  }
  return nums[left];
};

# 搜索旋转排序数组 (opens new window)(高频 ❤️❤️❤️)

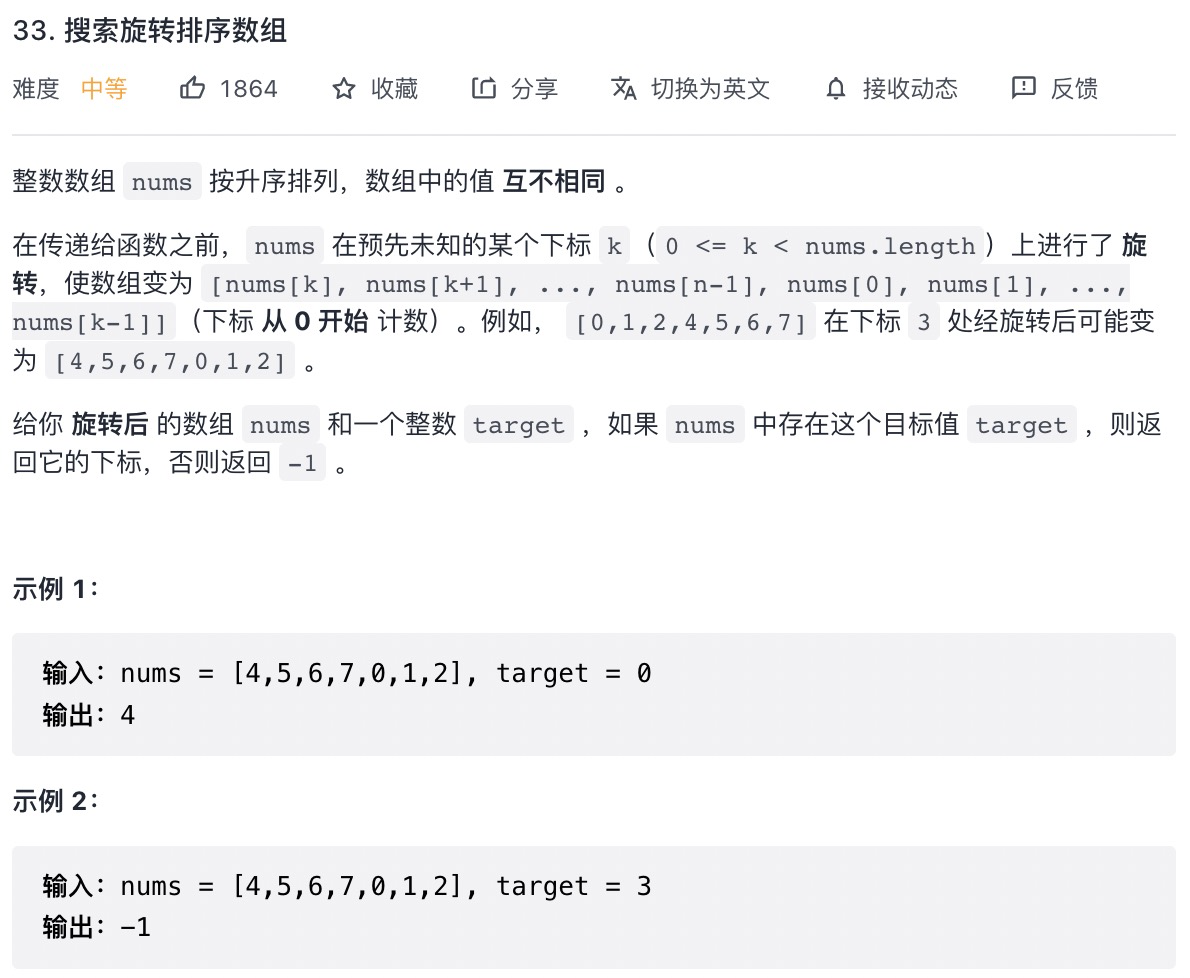
# 最长连续序列 (opens new window)(高频 ❤️❤️❤️)

/**
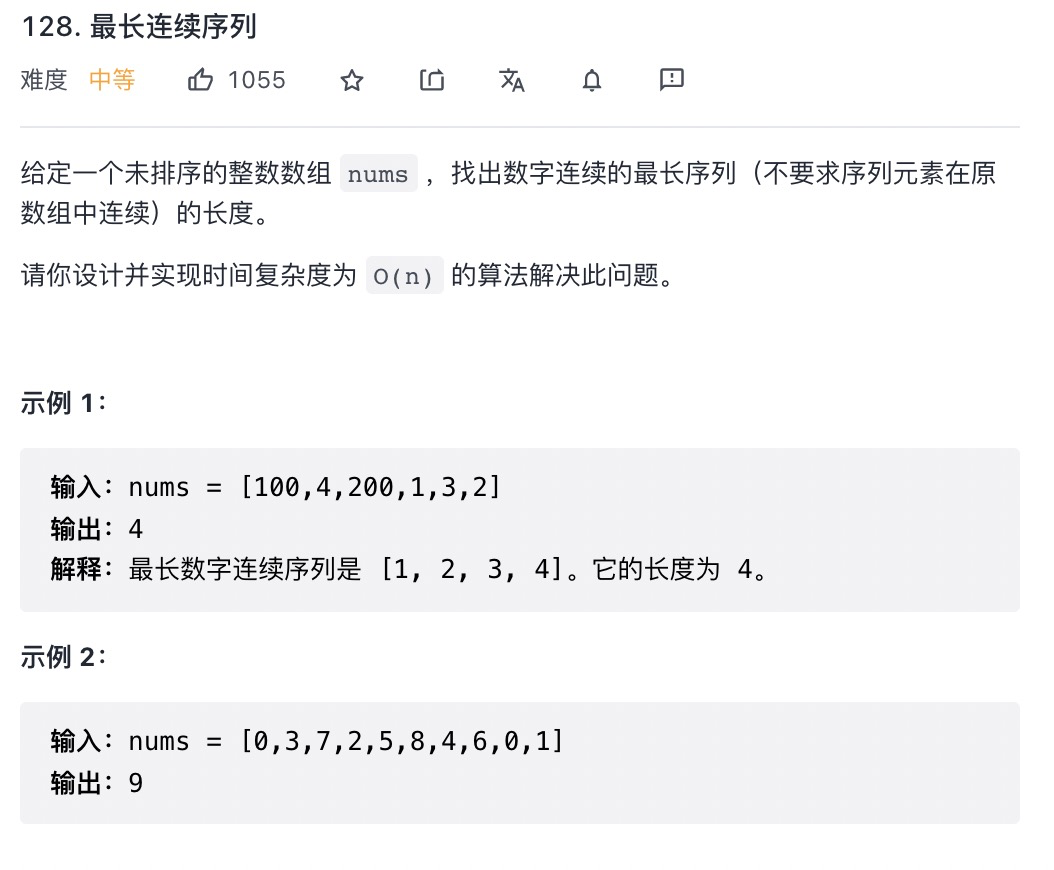
 * @param {number[]} nums
 * @return {number}
 */
var longestConsecutive = function(nums) {
  // 集合扩散查找
  let set = new Set(nums);
  let maxLength = 0;

  for (let num of set) {
    let len = 1;
    let left = num - 1;
    let right = num + 1;

    // 向左右扩散
    while (set.has(left)) {
      //找到就删掉，避免重复遍历，导致超时
      set.delete(left);
      left--;
      len++;
    }
    while (set.has(right)) {
      set.delete(right);
      right++;
      len++;
    }
    maxLength = Math.max(maxLength, len);
  }
  return maxLength;
};

# N 数之和

# 两数之和 (opens new window)(高频 ❤️❤️❤️)

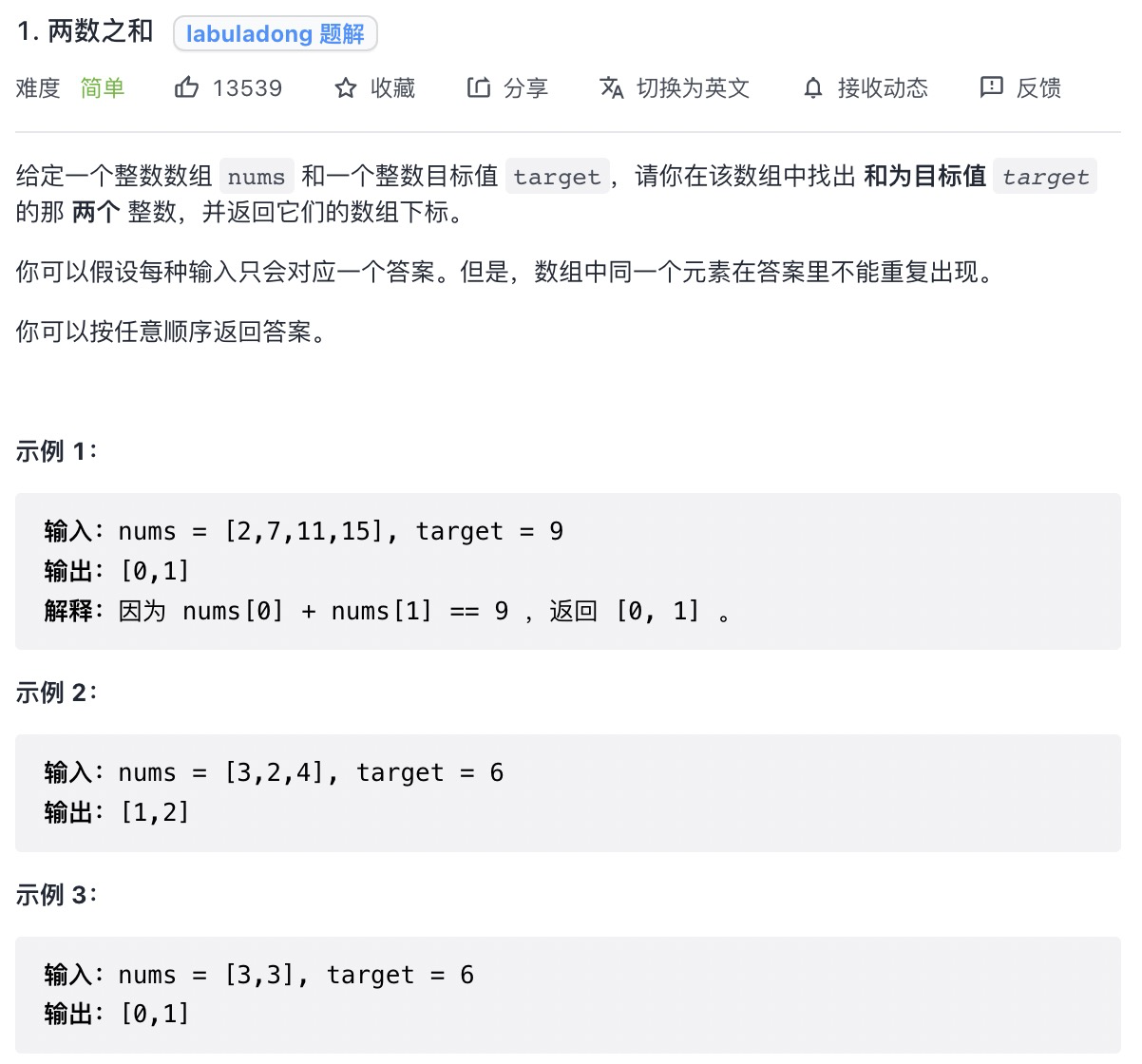看清楚题目，数组不是有序的，不要用二分法做

这道题可以巧妙利用map数据结构

map存入key为减剩下的数(而这个数一定是2，也就是接下来会出现的数)，value为下标

然后遍历到下几个元素，只需要比对map的key等不等于当前元素即可，相等直接返回`[map的value(第一个数)，i(第二个数)]`

var twoSum = function(nums, target) {
  let map = new Map();
  for (let i = 0; i < nums.length; i++) {
    if (map.has(nums[i])) {
      return [map.get(nums[i]), i];
    } else {
      map.set(target - nums[i], i);
    }
  }
};

# 两数之和 II - 输入有序数组 (opens new window)(高频 ❤️❤️❤️)

二分法

var twoSum = function(numbers, target) {
  let left = 0;
  let right = numbers.length - 1;
  while (left < right) {
    let sum = numbers[left] + numbers[right];
    if (sum === target) {
      return [left + 1, right + 1];
    } else if (sum < target) {
      // 让sum大点
      left++;
    } else if (sum > target) {
      // 让sum小点
      right--;
    }
  }
  return [-1, -1];
};

# 三数之和 (opens new window)(高频 ❤️❤️❤️)

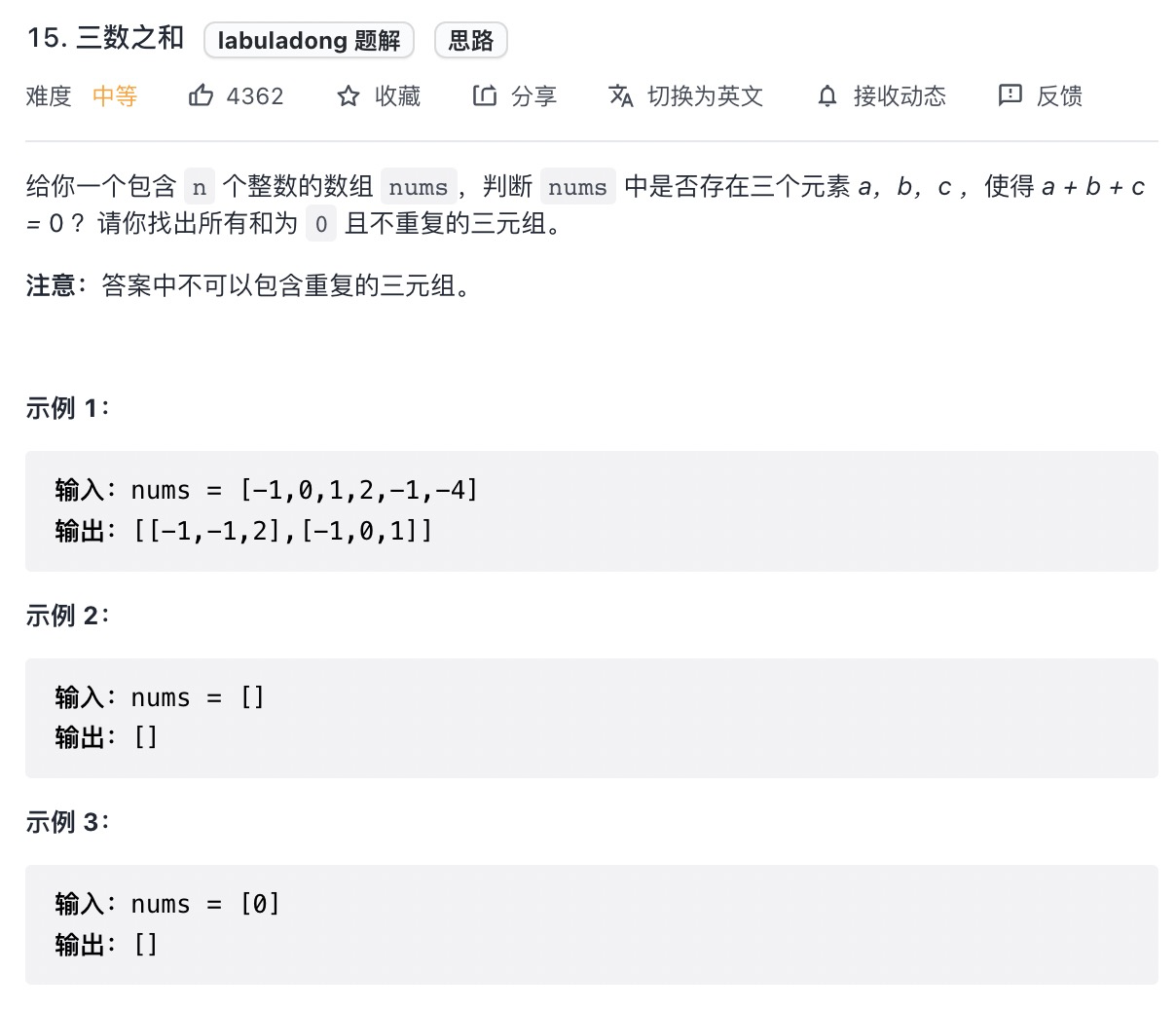
var threeSum = function(nums) {
  /**
   * 思路：想要计算三个数相加等于0，其实就是要找一个数以外的两个数相加等于他的负数
   * nums[i] - nums[i] = 0
   * 可以利用twoSum计算出另外两个数之和等于 -nums[i]即可
   */
  const twoSum = (nums, target) => {
    const result = [];
    const map = new Map();
    for (let i = 0; i < nums.length; i++) {
      if (map.has(nums[i])) {
        result.push([nums[map.get(nums[i])], nums[i]]);
      } else {
        map.set(target - nums[i], i);
      }
    }
    return result;
  };
  nums.sort((a, b) => a - b);
  let results = [];
  let newSet = new Set();
  for (let i = 0; i < nums.length - 2; i++) {
    let find = twoSum(nums.slice(i + 1), -nums[i]);
    if (find) {
      find.forEach(arr => {
        if (!newSet.has(arr.join(""))) {
          results.push([nums[i], ...arr]);
        }
        newSet.add(arr.join(""));
      });
    }
  }
  return results;
};

# 滑动窗口

# 最小覆盖子串 (opens new window)(高频 ❤️❤️❤️)

var minWindow = function(s, t) {
  // 前期初始化数据
  let left = 0;
  let right = 0;
  let need = new Map();
  for (let c of t) {
    need.set(c, need.has(c) ? need.get(c) + 1 : 1);
  }
  let needSize = need.size;
  let res = "";
  while (right < s.length) {
    let c1 = s[right];
    //右滑，更新数据
    if (need.has(c1)) {
      need.set(c1, need.get(c1) - 1);
      if (need.get(c1) === 0) {
        needSize--;
      }
    }

    /*
     * 当目标子串已经完全覆盖，也代表needSize=0，左滑,
     * 更新(将value+1,也就是慢慢删除覆盖子串)数据和返回数据
     * */

    while (needSize == 0) {
      const newStr = s.substring(left, right + 1);
      // 保证第一次赋值，并且每次更新返回值
      if (!res || res.length > newStr.length) {
        res = newStr;
      }
      let c2 = s[left];
      need.set(c2, need.get(c2) + 1);
      if (need.get(c2) === 1) {
        needSize++;
      }
      left++;
    }
    right++;
  }
  return res;
};

# 字符串的排列 (opens new window)

var checkInclusion = function(s1, s2) {
  /**
   * 初始化: need = {'a':1,'b':1} left=0 right=0 needSize = 2，res=false
   *
   * 右指针需做事情: 滑动指针，如果need碰到集合中有当前遍历字符， 更新need,更新needSize
   *
   * 左指针需做事情: 滑动指针，如果need碰到集合中有当前字符，更新need和needSize，在这之前更新res，
   * 如果窗口大小的等于s1的大小，则代表完全覆盖，res=true
   *
   * 左指针滑动的条件: needSize = 0
   */

  let left = 0;
  let right = 0;
  let need = new Map();
  // 初始化need
  for (let c of s1) {
    need.set(c, need.has(c) ? need.get(c) + 1 : 1);
  }
  let needSize = need.size;
  while (right < s2.length) {
    let c1 = s2[right];
    // 右滑，当前字符在need中
    if (need.has(c1)) {
      // 更新need,value - 1
      need.set(c1, need.get(c1) - 1);
      // 更新needSize
      if (need.get(c1) === 0) {
        needSize--;
      }
    }
    // 移动左指针
    while (needSize === 0) {
      // 更新最终结果
      if (right - left + 1 === s1.length) {
        return true;
      }
      let c2 = s2[left];
      // 左滑，更新need
      if (need.has(c2)) {
        need.set(c2, need.get(c2) + 1);
      }
      // 更新needSize
      if (need.get(c2) === 1) {
        needSize++;
      }
      left++;
    }
    // 这里的right指针位置具有玄学
    right++;
  }
  return false;
};

# 找到字符串中所有字母异位词 (opens new window)

var findAnagrams = function(s, p) {
  let left = 0;
  let right = 0;
  let need = new Map();
  for (let c of p) {
    need.set(c, need.has(c) ? need.get(c) + 1 : 1);
  }
  let needSize = need.size;
  let res = [];
  while (right < s.length) {
    let c1 = s[right];
    if (need.has(c1)) {
      need.set(c1, need.get(c1) - 1);
      if (need.get(c1) === 0) {
        needSize--;
      }
    }
    while (needSize === 0) {
      let c2 = s[left];
      if (right - left + 1 === p.length) {
        res.push(left);
      }
      if (need.has(c2)) {
        need.set(c2, need.get(c2) + 1);
        if (need.get(c2) === 1) {
          needSize++;
        }
      }
      left++;
    }
    right++;
  }
  return res;
};

# 无重复字符的最长子串长度 (opens new window)(高频 ❤️❤️❤️)

维护滑动窗口，右滑字符插入，更新返回值，然后左指针碰到已有元素，左指针就等于 map 中已有元素的 value+1。直到右指针遍历完成

var lengthOfLongestSubstring = function(s) {
  let left = 0;
  let map = new Map();
  let res = 0;
  for (let right = 0; right < s.length; s++) {
    // 如果碰到已有元素，则代表出现重复字符，左指针要改变指向
    // 满足左指针不越位，然后赋值
    if (map.has(s[right]) && map.get(s[right]) >= left) {
      left = map.get(s[right]) + 1;
    }
    map.set(s[r], r);
    res = Math.max(res, right - left + 1);
  }
  return res;
};

# 滑动窗口最大值 (opens new window)(高频 ❤️❤️❤️)

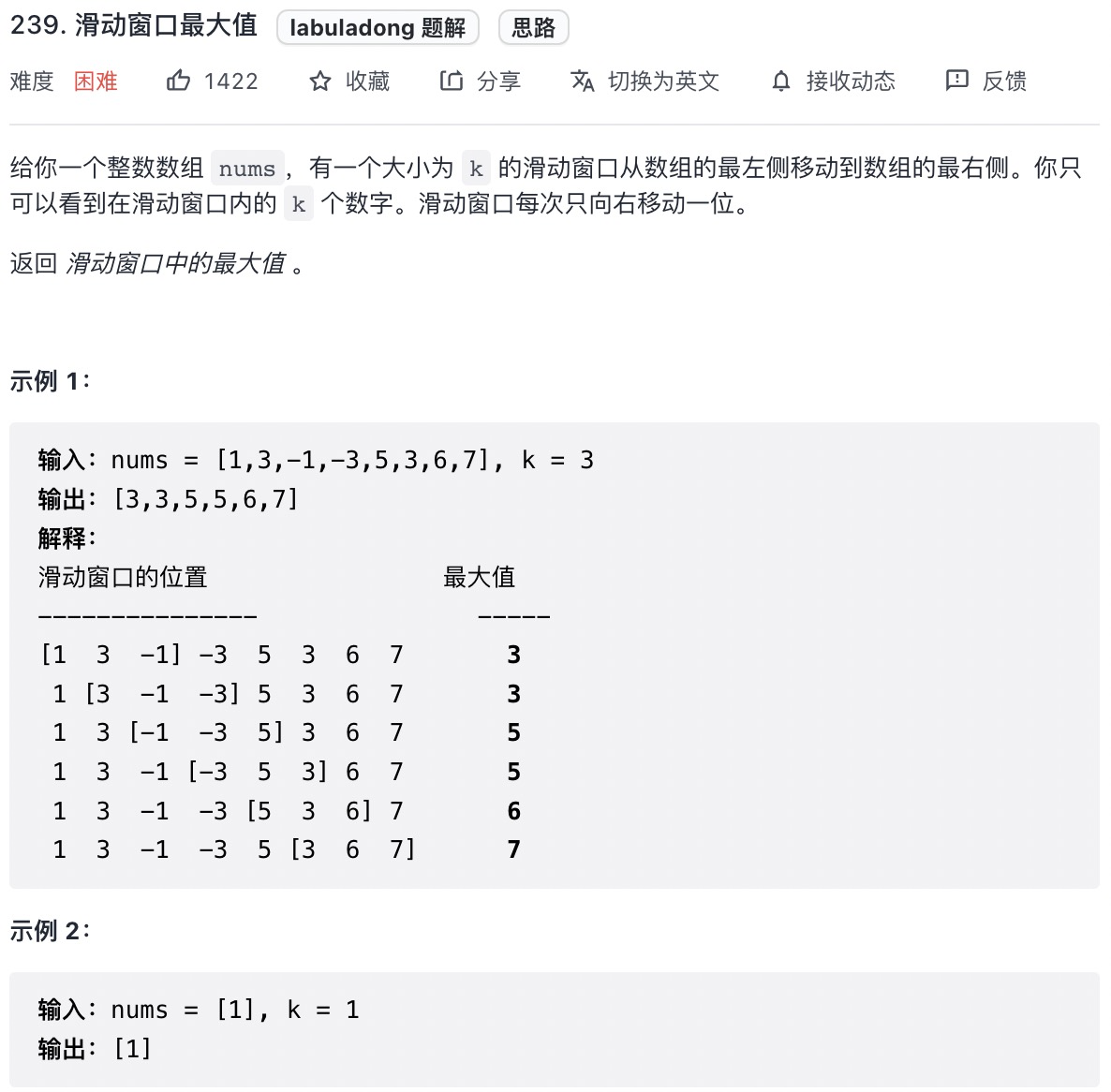
var maxSlidingWindow = function(nums, k) {
  /**
   * 思路：
   * 1. 使用滑动窗口解决该问题,每次移动找到窗口内的最大值，左右指针都移动 时间复杂度为O(nk) 可能会超时
   * 2. 双向队列解决该问题，将窗口视为递减队列，每次移动窗口，将窗口的最大值(this.deque[0])推入结果集，推入队列也就是push方法，需要保证推入的新值是小于队列的值的，否则删除掉小于它的数，最大值入队之后需要更新队列，也就是删除掉队列之前窗口之外的数 nums[i-k+1],删除的时候需要判断下删除的值是否和当前对头元素相等。最后返回结果集
   */
  // 滑动窗口思想
  // if(!nums.length || k===0){
  //     return []
  // }
  // let left = 0
  // let right = k -1
  // // 初始化结果集
  // let res = [findMax(nums,left,right)]
  // while(right < nums.length - 1){
  //     right++
  //     left++
  //     res.push(findMax(nums,left,right))
  // }
  // // 寻找窗口最大值
  // function findMax(nums,left,right){
  //     let max = -Infinity
  //     for(let i = left;i<=right;i++){
  //         max = Math.max(max,nums[i])
  //     }
  //     return max
  // }
  // return res

  // 双向队列思想
  class MaxDeque {
    constructor() {
      this.deque = [];
    }
    // 首先删除掉比插入元素还小的数，然后插入
    push(val) {
      while (this.deque.length > 0 && this.deque[this.deque.length - 1] < val) {
        this.deque.pop();
      }
      this.deque.push(val);
    }
    // 删除前需要检验下当前对头是否和val相等
    pop(val) {
      if (this.deque[0] === val) {
        this.deque.shift();
      }
    }
    max() {
      return this.deque[0];
    }
  }
  let window = new MaxDeque();
  let res = [];
  for (let i = 0; i < nums.length; i++) {
    // 先初始化窗口数据
    if (i < k - 1) {
      window.push(nums[i]);
    } else {
      // 移动窗口
      window.push(nums[i]);
      res.push(window.max());
      // 删除虽然在队列中，但是最大值更新了，所以需要删除掉的左侧元素,左侧元素的下标为i-k+1
      window.pop(nums[i - k + 1]);
    }
  }
  return res;
};

# 长度最小的子数组 (opens new window)

var minSubArrayLen = function(s, nums) {
  /**
   * 暴力枚举
   */
  let min = Infinity;
  for (let i = 0; i < nums.length; i++) {
    let sum = 0;
    for (let j = i; j < nums.length; j++) {
      sum += nums[j];
      if (sum >= s) {
        min = Math.min(j - i + 1, min);
        // 如果最小值为1 立即返回
        if (min === 1) {
          return min;
        }
        // 下标 j 作为数组的右边界从 0 开始不停向后扩展，每往后一位，就把本次的求和加上新的数字，只要本轮循环的和大于 s，就应该停止循环，因为没必要再往后扩展了，往后扩展的数组长度一定是大于当前长度的
        break;
      }
    }
  }
  return min === Infinity ? 0 : min;
};

# 动态规划

# 斐波那契数 (opens new window)(高频 ❤️❤️❤️)

// dp[n] ：输入n返回对应的斐波那契额数
var fib = function(n) {
  let dp = [0, 1, 1];
  for (let i = 3; i <= n; i++) {
    dp[i] = dp[i - 1] + dp[i - 2];
  }
  return dp[n];
};

# 零钱兑换 (opens new window)(高频 ❤️❤️❤️)

var coinChange = function(coins, amount) {
  /**
   * 1. 初始化dp
   * 2. 初始化base-case
   * 3. for循环所有的状态取值
   * 4. dp[状态] = 求最值(选择1，选择2,...)
   * dp[n] ：输入需要凑的目标金额n，要求返回能够达到凑出来的金额等于n的最小硬币数量
   */
  // amount+1 作为上限值
  let dp = Array(amount + 1).fill(amount + 1);
  dp[0] = 0;
  for (let i = 0; i < dp.length; i++) {
    for (const coin of coins) {
      // 子问题不成立的情况
      if (i - coin < 0) {
        continue;
      }
      // 如果满足条件 dp[i]就等于1+dp[i-coin]和自己的最小值,i-coin代表剩余需要凑的金额，+1代表数量+1
      dp[i] = Math.min(dp[i], 1 + dp[i - coin]);
    }
  }
  // 满足不能越界
  return dp[amount] === amount + 1 ? -1 : dp[amount];
};

# 零钱兑换 2 (opens new window)

// amount = 5, coins = [1, 2, 5] 输出总方案数
var change = function(amount, coins) {
  var dp = new Array(amount + 1).fill(0);
  dp[0] = 1;
  for (let coin of coins) {
    for (let i = coin; i < amount + 1; i++) {
      //从0开始递推
      dp[i] = dp[i] + dp[i - coin];
    }
  }

  return dp[amount];
};
console.log(change(24, [1, 2, 5, 10, 20, 50, 70]));

# 爬楼梯 (opens new window)(高频 ❤️❤️❤️)

var climbStairs = function(n) {
  // dp[n] :代表n阶楼梯可以有几种爬法
  // base-case
  let dp = [0, 1, 2];
  for (let i = 3; i <= n; i++) {
    dp[i] = dp[i - 1] + dp[i - 2];
  }
  return dp[n];
};

# 打家劫舍 (opens new window)(高频 ❤️❤️❤️)

var rob = function(nums) {
  /**
   * dp[i]表示盗窃[0...i-1]号房子的最大价值,我们求的结果就是dp[n-1]
   * dp[i] = Math.max(dp[i-1],dp[i-2] + nums[i]):
   * 这个等式怎么来的，我们假设第i号房子盗取，则盗窃到这号房子的最大价值为dp[i-2]+ nums[i],因为相邻房子不能盗取；如果不盗取i号房子，则dp[i]和dp[i-1]是相同的。这两种取最大值即可得出方程
   *
   * 举例说明: nums = [2,4,3],1号房子可盗窃最大价值就是本身nums[0]=2,2号房子可盗窃最大价值也是本身nums[1] = 4,3号房子可盗窃的最大价值dp[2] = Math.max(4,2+3) = 5,状态转移方程成立
   *  */
  let n = nums.length;
  // base-case
  if (!n) {
    return 0;
  }
  if (n === 1) {
    return nums[0];
  }
  let dp = [];
  // 需要列举出dp[0] 和dp[1]的特殊情况
  dp[0] = nums[0];
  dp[1] = Math.max(nums[0], nums[1]);
  for (let i = 2; i <= n; i++) {
    dp[i] = Math.max(dp[i - 1], dp[i - 2] + nums[i]);
  }
  return dp[n - 1];
};

# 打家劫舍 II (opens new window)🥇

这里和上面那道题的唯一区别就是首尾不能共存，所以需要分别剔除首尾

var rob = function(nums) {
  /**
   * 和打家劫舍一相比：这里需要分别剔除首尾的房子，然后比较两种情况的到最大金额的最大值
   *  */

  // 这里判空需要写在函数外面，否则会报错
  if (!nums.length) {
    return 0;
  }
  if (nums.length === 1) {
    return nums[0];
  }
  function getRes(arr) {
    let n = arr.length;
    let dp = [];
    // base-case
    dp[0] = arr[0];
    dp[1] = Math.max(arr[0], arr[1]);
    for (let i = 2; i <= n; i++) {
      dp[i] = Math.max(dp[i - 1], dp[i - 2] + arr[i]);
    }
    return dp[n - 1];
  }
  // 由于首尾不能共存，分别剔除首尾
  let shiftArray = JSON.parse(JSON.stringify(nums));
  shiftArray.shift();
  let res1 = getRes(shiftArray);
  let popArray = JSON.parse(JSON.stringify(nums));
  popArray.pop();
  let res2 = getRes(popArray);
  return Math.max(res1, res2);
};

# 打家劫舍 III (opens new window)🥇

var rob = function(root) {
  /**
   * 使用后续遍历
   * dp就两个元素，一个是根结点偷的结果，一个是根结点不偷的结果
   * dp(0) 代表以node结点为根结点的树，node结点不偷的最高金额，dp(1)为偷
   * 1. 如果根结点偷了，左右子树均不能偷
   * 2. 如果根结点没偷，则左右子树偷或者不偷，取最大值,可以同时偷
   */
  const dfs = node => {
    if (!node) {
      return [0, 0];
    }
    let left = dfs(node.left);
    let right = dfs(node.right);
    let dp = Array(2);
    // 分为偷和不偷两种情况，归类到最后的返回数组
    dp[0] = Math.max(left[0], left[1]) + Math.max(right[0], right[1]);
    dp[1] = node.val + left[0] + right[0];
    return dp;
  };
  let res = dfs(root);
  return Math.max(res[0], res[1]);
};

# 目标和 (opens new window)🥇

首先可以利用回溯算法求出解，然后使用备忘录优化,最后还可以转为动态规划问题里面的 0-1 背包问题

var findTargetSumWays = function(nums, S) {
  if (!nums.length) {
    return 0;
  }
  /**
   * 回溯算法解法
   */
  //    let result = 0
  //    // 路径，当前选择下标，剩余的target值
  //    function backtrack(track,index,res){
  //        // 终止递归条件
  //        if(index === track.length){
  //            if(res === 0){
  //                // 满足条件
  //                result++
  //            }
  //            return result
  //        }
  //        // 当选择-号，剩余值应该增加nums[index]
  //        res+=track[index]
  //        backtrack(track,index+1,res)
  //        // 撤销选择
  //        res-=track[index]
  //        res-=track[index]
  //        backtrack(track,index+1,res)
  //        res+=track[index]
  //    }
  //    backtrack(nums,0,S)
  //    return result

  /**
   * 添加备忘录解法
   */
  const map = new Map();
  function dp(nums, index, res) {
    // dp(nums,index,res) 代表 nums数组中从index下标开始选择-1或者+1对其元素进行累加，最后使得结果和target相等时的方法数
    if (index === nums.length) {
      // 累加到最后的剩余值为0时，返回1，否则返回0
      if (!res) {
        return 1;
      }
      return 0;
    }
    let key = `${index}-${res}`;
    if (map.has(key)) {
      return map.get(key);
    }
    // 穷举法 加起来
    const result = dp(nums, index + 1, res + nums[index]) + dp(nums, index + 1, res - nums[index]);
    map.set(key, result);
    return result;
  }
  return dp(nums, 0, S);
};

# 青蛙跳台阶问题 (opens new window)

function fn3(n) {
  const dp = [1, 1];
  for (let i = 2; i <= n; i++) {
    dp[i] = (dp[i - 1] + dp[i - 2]) % 1000000007;
  }
  return dp[n];
}

# 最长递增子序列问题 (opens new window)(高频 ❤️❤️❤️)

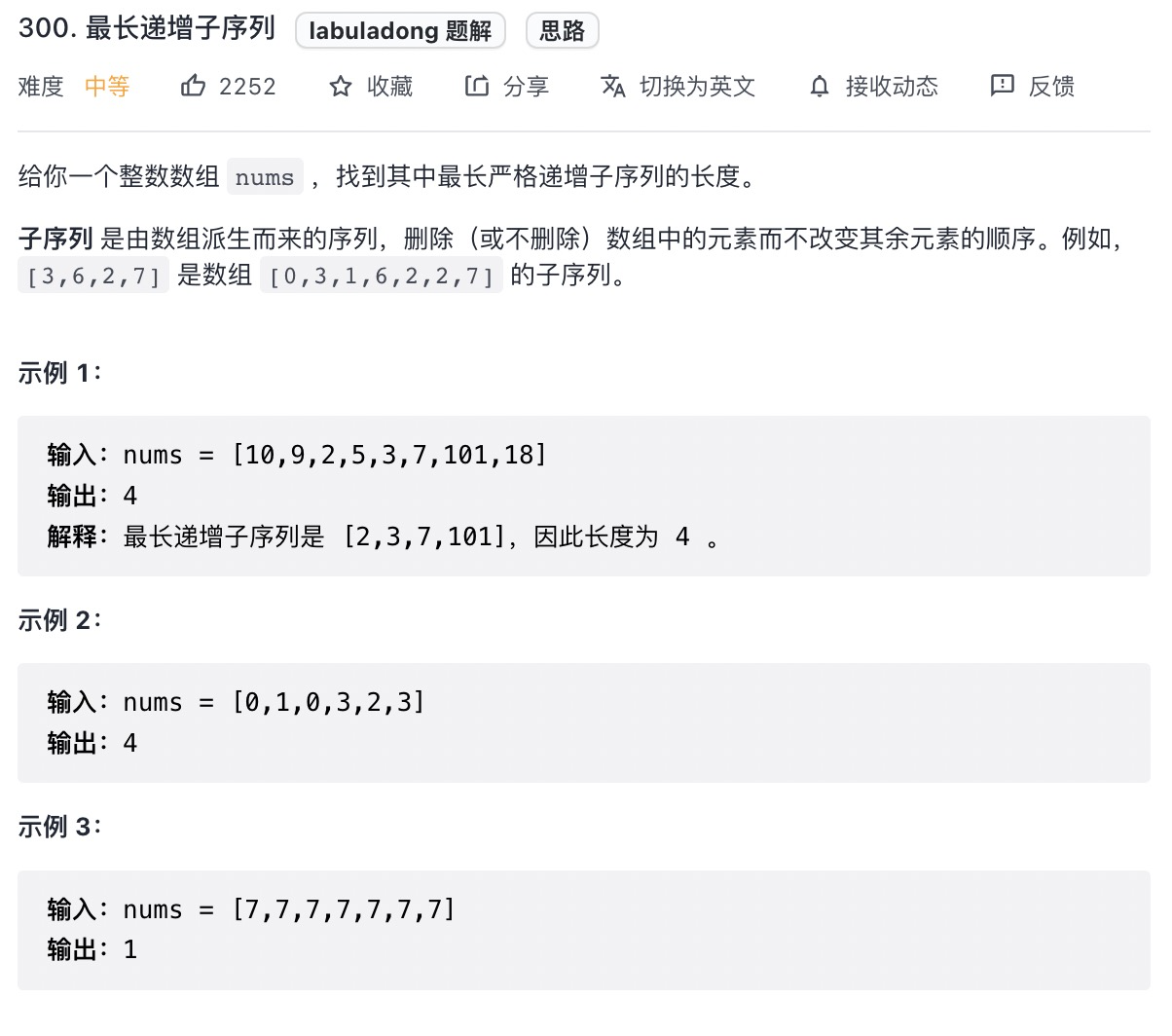
- 遍历到 nums[i] 时，需要把下标 i 之前的所有的数都看一遍；
- 只要 nums[i] 严格大于在它位置之前的某个数，那么 nums[i] 就可以接在这个数后面形成一个更长的上升子序列；
- 因此，dp[i] 就等于下标 i 之前严格小于 nums[i] 的状态值的最大者 +1

dp[i] 就等于下标 i 之前严格小于 nums[i] 的状态值的最大者 +1

function lengthOfLIS(nums) {
  // dp[n] 代表以nums[n]结尾的最长子序列长度，也就是左右子序列里面最长的长度
  let n = nums.length;
  // base-case
  if (!n) {
    return 0;
  }
  if (n === 1) {
    return 1;
  }
  // 假设每一个下标对应的元素都为1，默认长度为1
  let dp = Array(n).fill(1);
  // 双层循环，i代表选中子序列的最后一个数，j代表在它之前的数，在它之前的数必须小于第i个元素,0<=j<i
  for (let i = 1; i < nums.length; i++) {
    for (let j = 0; j < i; j++) {
      if (nums[j] < nums[j]) {
        // dp[i] 就等于下标 i 之前严格小于 nums[i] 的状态值的最大者 +1
        dp[i] = Math.max(dp[i], dp[j] + 1);
      }
    }
  }
  // 现在dp是个数组，里面存着每个下标所对应的子序列长度，取最大值即可
  return Math.max(...dp);
}

# 最大连续子数组和 (opens new window)(高频 ❤️❤️❤️)

var maxSubArray = function(nums) {
  /**
   * dp[i] "以nums[i]结尾的最大子数组和"
   * 如果dp[i-1]<=0 ，则产生负效果，此时dp[i] = nums[i]
   * 如果dp[i-1]>=0 ，则产生曾效果，此时dp[i] = dp[i-1] + nums[i]
   */
  let n = nums.length;
  if (!n) {
    return 0;
  }
  let dp = Array(n);
  // base-case
  dp[0] = nums[0];
  // 假设数组最大值为第一个元素
  let maxSum = nums[0];
  for (let i = 1; i < nums.length; i++) {
    if (dp[i - 1] <= 0) {
      // 累加产生负效果 直接等于nums[i]
      dp[i] = nums[i];
    } else {
      dp[i] = dp[i - 1] + nums[i];
    }
    maxSum = Math.max(maxSum, dp[i]);
  }
  return maxSum;
};

# 买卖股票的最佳时机 (opens new window)(高频 ❤️❤️❤️)

dp[3][2][1]的含义就是：今天是第三天，我现在手上持有着股票，至今最多进行 2 次交易的最大利润

思路详见模板

/**
 * base-case:
 *   dp[i][0][0] = 0 第i天，0次交易，没有股票 利益为0
 *   dp[i][0][1] = -Infinity 第i天 0次交易 有股票 利益为负无穷
 * dp 方程
 *   dp[i][k][0] = Math.max(dp[i-1][k][0],dp[i-1][k][1] + prices[i]) 第i天k次交易未持有股票，两种情况: 昨天未持有股票休息 昨天持有股票今天买了
 *   dp[i][k][1] = Math.max(dp[i-1][k][1],dp[i-1][k-1][0] - prices[i]) 第i天k次交易持有股票  两种情况: 昨天持有股票休息，昨天未持有股票今天买入
 *
 * O(1) 优化版
 *
 * dp_i_0 = Math.max(dp_i_0,dp_i_1 + prices[n])
 * dp_i_1 = Math.max(dp_i_1,-prices[n])
 *
 * 最小值求的结果就是dp_i_0
 * **/
var maxProfit = function(prices) {
  let dp_i_0 = 0;
  let dp_i_1 = -Infinity;
  for (let n = 0; n < prices.length; n++) {
    dp_i_0 = Math.max(dp_i_0, dp_i_1 + prices[n]);
    dp_i_1 = Math.max(dp_i_1, -prices[n]);
  }
  return dp_i_0;
};

# 买卖股票的最佳时机 II (opens new window)🥇

var maxProfit = function(prices) {
  let dp_i_0 = 0;
  let dp_i_1 = -Infinity;
  for (let i = 0; i < prices.length; i++) {
    dp_i_0 = Math.max(dp_i_0, dp_i_1 + prices[i]);
    dp_i_1 = Math.max(dp_i_1, dp_i_0 - prices[i]);
  }
  return dp_i_0;
};

# 买卖股票的最佳时机含手续费 (opens new window)🥇

var maxProfit = function(prices, fee) {
  let dp_i_0 = 0;
  let dp_i_1 = -Infinity;
  for (let i = 0; i < prices.length; i++) {
    dp_i_0 = Math.max(dp_i_0, dp_i_1 + prices[i]);
    dp_i_1 = Math.max(dp_i_1, dp_i_0 - prices[i] - fee);
  }
  return dp_i_0;
};

# 最佳买卖股票时机含冷冻期 (opens new window)🥇

var maxProfit = function(prices) {
  let dp_i_0 = 0;
  let dp_i_1 = -Infinity;
  let dp_pre_0 = 0; // 相当于 dp[i-2][0]
  for (let i = 0; i < prices.length; i++) {
    // 记录上次的最大利润
    let temp = dp_i_0;
    dp_i_0 = Math.max(dp_i_0, dp_i_1 + prices[i]);
    dp_i_1 = Math.max(dp_i_1, dp_pre_0 - prices[i]);
    dp_pre_0 = temp;
  }
  return dp_i_0;
};

# 最长回文子串 (opens new window)(高频 ❤️❤️❤️)

使用中心扩散思想，以如果是奇数串以 **s[i]** 为中心点，如果是偶数串则以 **s[i]**和**s[i+1]** 为中心点，然后向两边扩散范围

let longestPalindrome = function(s) {
  let n = s.length;
  if (n < 2) {
    return s;
  }
  // 定义最大值为1，开始下标为0
  let begin = 0;
  let max = 1;
  // 扩散方法,传入头和尾下标
  let spread = (start, end) => {
    while (s[start] === s[end] && start >= 0 && end < n) {
      // 此时窗口的大小
      let len = end - start + 1;
      // 窗口大于最大值时，更新最大值和起始点
      if (len > max) {
        max = len;
        begin = start;
      }
      start--;
      end++;
    }
  };

  // 遍历字符串,考虑两种情况
  for (let mid = 0; mid < n; mid++) {
    spread(mid, mid);
    spread(mid, mid + 1);
  }
  return s.substr(begin, max);
};

# 最长公共子序列 (opens new window)(高频 ❤️❤️❤️)

思路： https://mp.weixin.qq.com/s/ZhPEchewfc03xWv9VP3msg

var longestCommonSubsequence = function(text1, text2) {
  // 定义：s1[0..i-1] 和 s2[0..j-1] 的 lcs 长度为 dp[i][j]
  // 目标：s1[0..m-1] 和 s2[0..n-1] 的 lcs 长度，即 dp[m][n]
  // 如果s1[i] = s2[j] 则两个字符都在lcs中，长度加1；
  // 如果s1[i]!==s2[j]，则有三种情况，一种是s1[i]不在lcs，一种是s2[j]不在lcs,一种是都不在，这种可以忽略
  // base case: dp[0][..] = dp[..][0] = 0
  let m = text1.length;
  let n = text2.length;
  const dp = Array.from(Array(m + 1), () => Array(n + 1).fill(0));
  // 注意这里下标需要从1开始，最后一个元素可取
  for (let i = 1; i <= m; i++) {
    for (let j = 1; j <= n; j++) {
      // 因为下标是从1开始的
      let str1 = text1[i - 1];
      let str2 = text2[j - 1];
      if (str1 === str2) {
        dp[i][j] = 1 + dp[i - 1][j - 1];
      } else {
        dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
      }
    }
  }
  return dp[m][n];
};

# 两个字符串的删除操作 (opens new window)🥇

var minDistance = function(word1, word2) {
  // 思路： 找到最大公共子序列，然后除去这两个子序列的长度即为所求
  let m = word1.length;
  let n = word2.length;
  let dp = Array.from(Array(m + 1), () => Array(n + 1).fill(0));
  for (let i = 1; i <= m; i++) {
    for (let j = 1; j <= n; j++) {
      let s1 = word1[i - 1];
      let s2 = word2[j - 1];
      if (s1 === s2) {
        dp[i][j] = 1 + dp[i - 1][j - 1];
      } else {
        dp[i][j] = Math.max(dp[i][j - 1], dp[i - 1][j]);
      }
    }
  }
  return m - dp[m][n] + n - dp[m][n];
};

# 最长重复子数组 (opens new window)(高频 ❤️❤️❤️)

// 思路:和最长公共子序列相同，dp[i][j] 代表s1[0...i-1]和s2[0...j-1]的公共部分的最大长度

var findLength = function(A, B) {
  let m = A.length;
  let n = B.length;
  let dp = Array.from(Array(m + 1), () => Array(n + 1).fill(0));
  let res = 0;
  for (let i = 1; i <= m; i++) {
    for (let j = 1; j <= n; j++) {
      let a = A[i - 1];
      let b = B[j - 1];
      if (a === b) {
        dp[i][j] = 1 + dp[i - 1][j - 1];
      }
      // 不等已经初始化
      res = Math.max(res, dp[i][j]);
    }
  }
  return res;
};

# 最小路径和 (opens new window)(高频 ❤️❤️❤️)

var minPathSum = function(grid) {
  /**
   * 思路: dp[i][j] = Math.min(dp[i-1][j],dp[i][j-1]) 代表到达(i，j)路径总和最小
   * 其实我们字需要考虑，走到的那一步也就是(i,j)是从哪里来的，只有两种可能
   * 1. 上方
   * 2. 左方
   * 所以可以推测出该动态规划方程，但是有两个特殊地方需要处理，第一行只能都是左方来的，第一列只能都是上方来的
   * 这里遍历记得从1开始，防止越界
   */
  let row = grid.length;
  let col = grid[0].length;
  // 处理第一行 使用grid数组代替dp数组也可以达到效果
  for (let j = 1; j < col; j++) {
    grid[0][j] += grid[0][j - 1];
  }
  // 处理第一列
  for (let i = 1; i < row; i++) {
    grid[i][0] += grid[i - 1][0];
  }
  // 处理常规行列
  for (let i = 1; i < row; i++) {
    for (let j = 1; j < col; j++) {
      grid[i][j] += Math.min(grid[i - 1][j], grid[i][j - 1]);
    }
  }
  return grid[row - 1][col - 1];
};

# 单词拆分 (opens new window)

动态规划解题

dp[i]：长度为 i 的 s[0:i-1]子串是否能拆分成单词。题目求:dp[s.length]

dp[i+1] 代表 s[0,....i]可以拆解单词，满足 s[length]可以被拆解的条件

dp[i-1] = true
s.slice(i,j) 存在单词库中
dp[0] = true

#

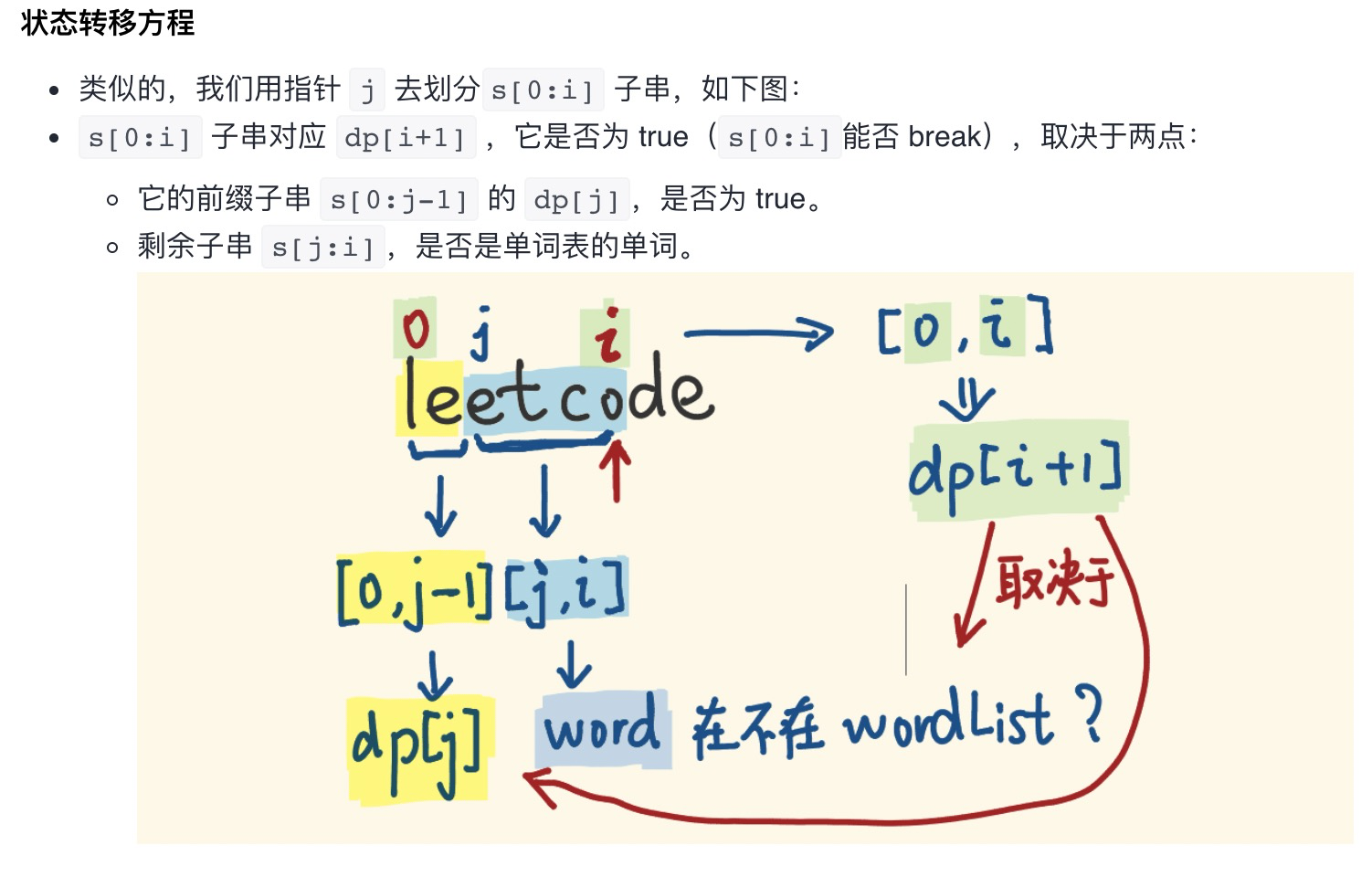
j 的取值范围在 0<=j<=i-1,因为要保证后缀单词存在

var wordBreak = function(s, wordDict) {
  // dp[i] 代表 s[0,....i-1] 可以被拆解
  let length = s.length;
  let dp = Array(length + 1).fill(false);
  let wordDictSet = new Set(wordDict);
  dp[0] = true;

  for (let i = 1; i <= length; i++) {
    for (let j = i - 1; j >= 0; j--) {
      let sliceWord = s.slice(j, i);
      // 0 ~ j-1 可被拆解 && j ~ i-1 存在单词库
      if (wordDictSet.has(sliceWord) && dp[j]) {
        dp[i] = true;
        break;
      }
    }
  }
  return dp[length];
};

# 不同路径 (opens new window)

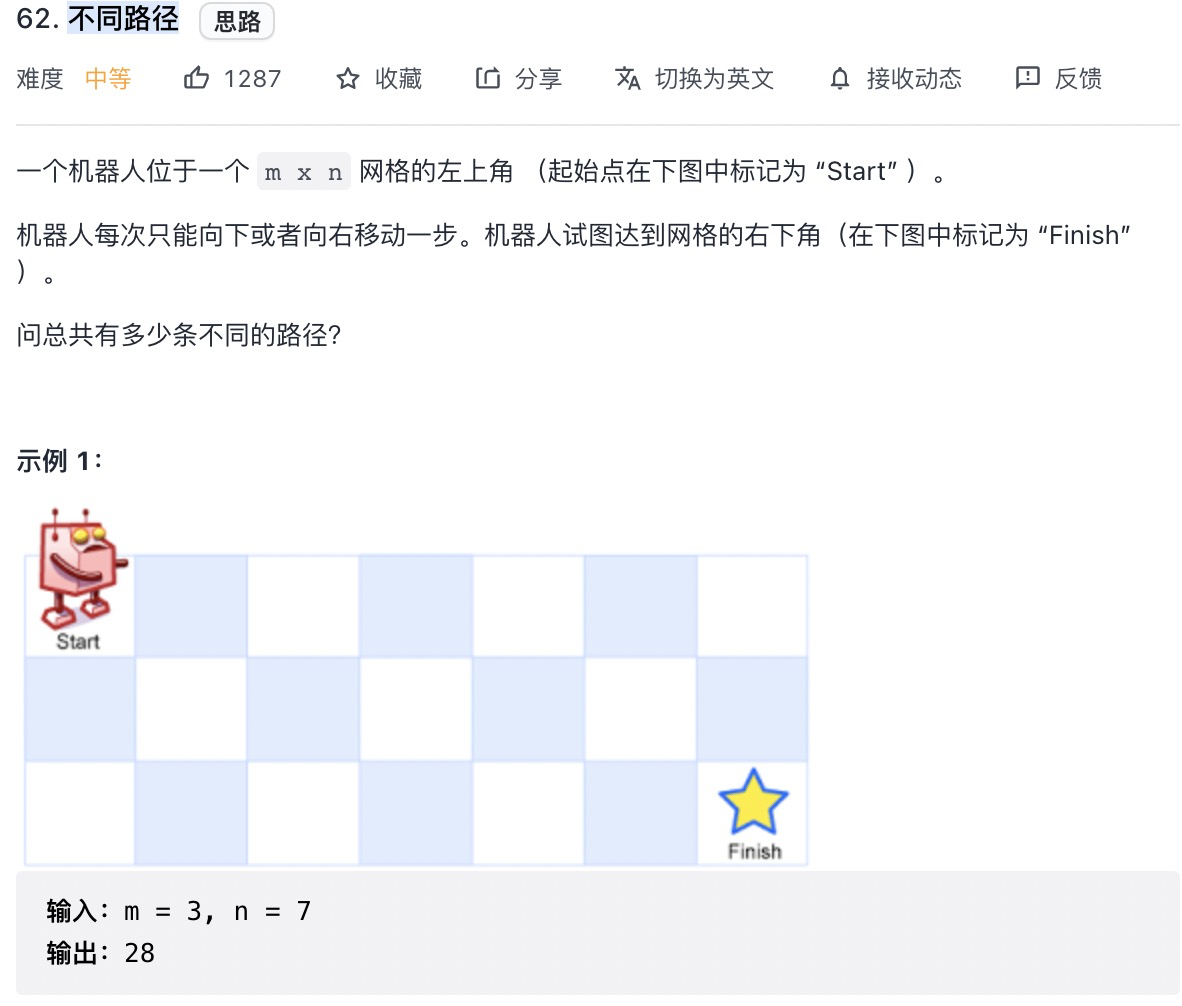
# 编辑距离 (opens new window)(高频 ❤️❤️❤️)

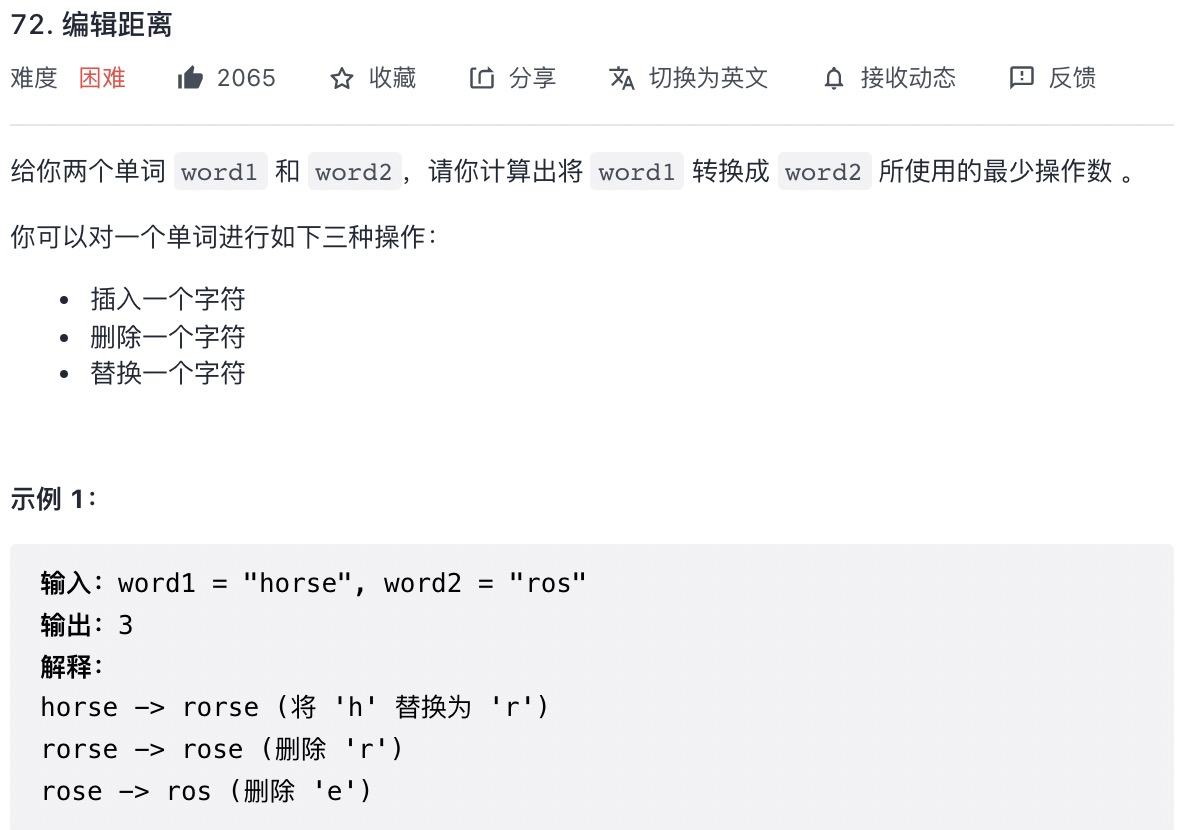
完整解题思路: https://leetcode-cn.com/problems/edit-distance/solution/dai-ma-sui-xiang-lu-72-bian-ji-ju-chi-do-y87e/

/**
 * @param {string} word1
 * @param {string} word2
 * @return {number}
 */
var minDistance = function(word1, word2) {
  let dp = Array.from(Array(word1.length + 1), () => Array(word2.length + 1).fill(0));
  /* base case 是i走完word1或j走完word2，可以直接返回另一个字符串剩下的长度 */
  // j走完word2 如果i还没走完word1，那么只能用删除操作把word1缩短为word2,也就是直接返回另一个字符串剩下的长度
  for (let i = 1; i <= word1.length; i++) {
    dp[i][0] = i;
  }
  // 同理  如果i走完word1时j还没走完了word2，那就只能用插入操作把word2剩下的字符全部插入word1
  for (let j = 1; j <= word2.length; j++) {
    dp[0][j] = j;
  }

  for (let i = 1; i <= word1.length; i++) {
    for (let j = 1; j <= word2.length; j++) {
      if (word1[i - 1] === word2[j - 1]) {
        // 啥也不做
        dp[i][j] = dp[i - 1][j - 1];
      } else {
        // 三选一  哪个操作最后得到的编辑距离最小，就选谁
        dp[i][j] = Math.min(
          // 删除
          // 直接把word1[i]这个字符删掉，前移i继续跟j对比   操作数+1
          dp[i - 1][j] + 1,
          // 插入
          // 直接在word1[i]插入一个和word2[j]一样的字符，那么word2[j]就被匹配了，前移j继续跟i对比
          dp[i][j - 1] + 1,
          // 替换
          // 直接把word1[i]替换成word2[j] 这样它俩就匹配了，同时前移i,j继续对比
          dp[i - 1][j - 1] + 1
        );
      }
    }
  }

  return dp[word1.length][word2.length];
};

# 贪心算法

# 分配饼干 (opens new window)

降序排序两个数组，用两个指针来分发饼干，将最大的饼干分给最贪婪的小朋友，如果能够开心则继续发下一个小朋友，否则无法满足，则放弃发这个小朋友，移动小朋友的指针即可

var findContentChildren = function(g, s) {
  // 内置的排序方法效率最好
  g = g.sort((a, b) => b - a);
  s = s.sort((a, b) => b - a);
  // 因为数组从大到小排序 通过控制两个数组的指针来分配饼干，其实下标为0
  let g1 = 0;
  let s1 = 0;
  let res = 0;
  while (g1 < g.length && s1 < s.length) {
    // 代表最大的饼干可以让最贪心的小朋友开心,更新数据
    if (s[s1] >= g[g1]) {
      res++;
      s1++;
      g1++;
    } else {
      // 最大的饼干无法满足最贪心小朋友
      g1++;
    }
  }
  return res;
};

# 无重叠区间 (opens new window)

解题思路：

var eraseOverlapIntervals = function(intervals) {
  /**
   * 整体思路： 适用贪心算法
   * 1. 首先在按照每个区间end从小到大排序的区间中调出第一个最小的区间 X
   * 2. 然后遍历整个集合，如果有一个区间的start是大于等于 X的end，也就是说当前区间起始位置在X区间的后面，那么当前区间和X区间是不重叠的
   * 3. 重复1,2,步，更新count和X即可
   */
  if (intervals.length === 0) {
    return 0;
  }
  // intervals是一个二维数组，根据end升序排列
  intervals = intervals.sort((a, b) => a[1] - b[1]);
  // 假设长度为1
  let count = 1;
  let end_x = intervals[0][1];
  for (const interval of intervals) {
    start = interval[0];
    // 判断start是否超过X的end, 不重叠
    if (start >= end_x) {
      count++;
      end_x = interval[1];
    }
  }
  return intervals.length - count;
};

# 合并区间 (opens new window)(高频 ❤️❤️❤️)

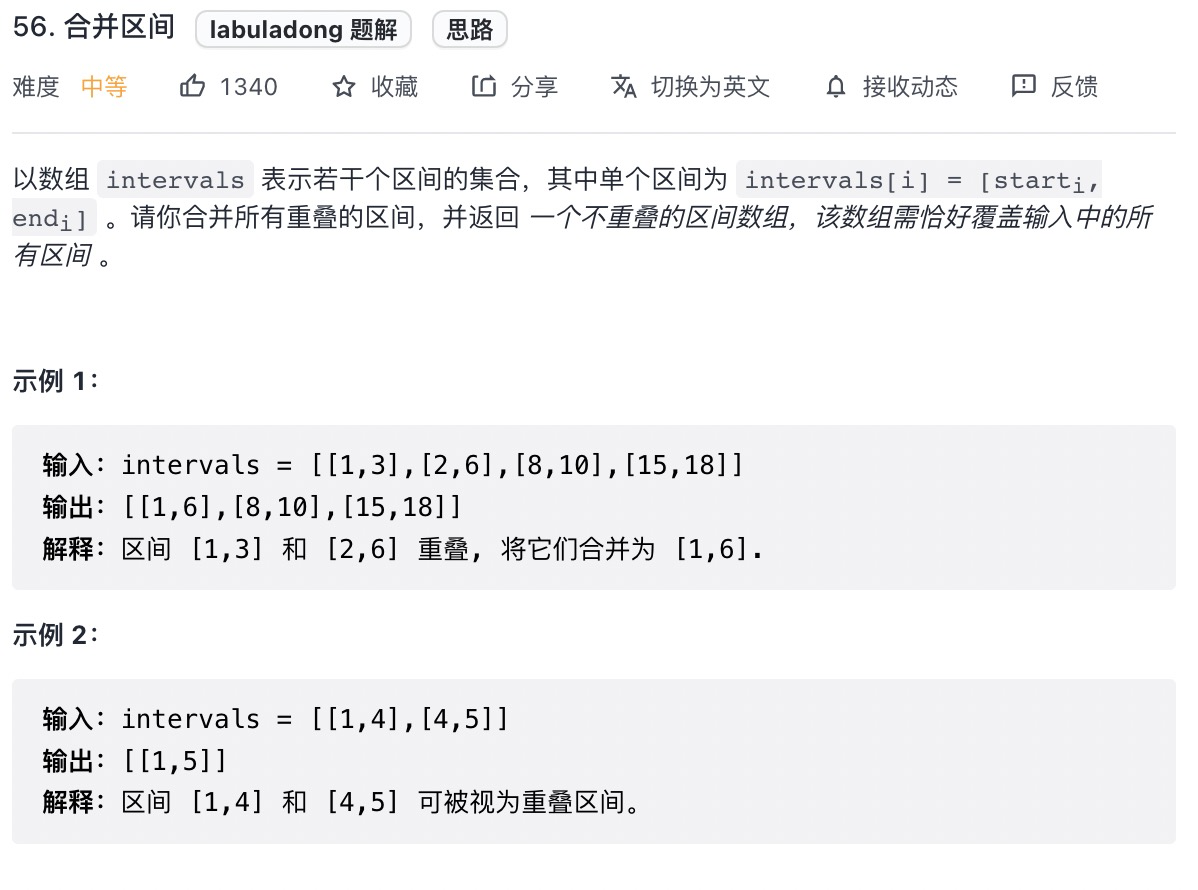
画张图更易理解

https://mp.weixin.qq.com/s/Eb6ewVajH56cUlY9LetRJw

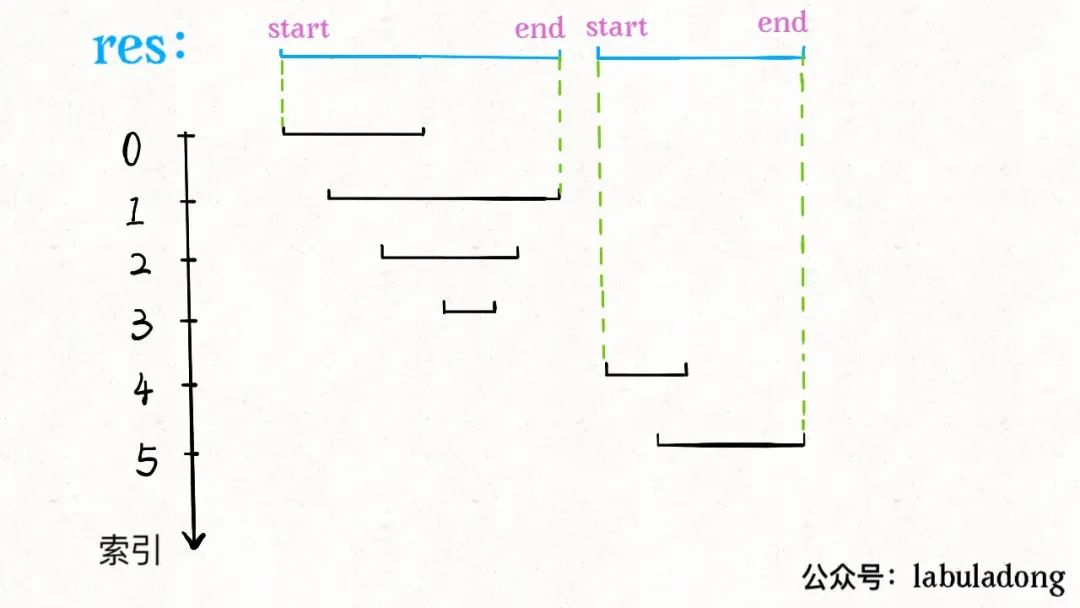
var merge = function(intervals) {
  /**
   * 首先假设两个两个数组pre，cur 需要按照start排序
   * 1. 如果pre[1] <= cur[0] 则代表两数组相交，这时需要合并区间，区间最小值就是pre[0],最大值为Math.max(pre[1],cur[1])
   * 2. 如果没有相交，则更新pre = cur，循环遍历下去，然后将pre保存到结果区间里即可
   * 3. 最后将结果push进res
   *  反正记住这里需要重复push两次pre到结果集就好了
   */
  if (intervals.length === 0) {
    return [];
  }
  intervals = intervals.sort((a, b) => a[0] - b[0]);
  let res = [];
  let pre = intervals[0];
  for (let i = 1; i < intervals.length; i++) {
    let cur = intervals[i];
    // 相交
    if (pre[1] >= cur[0]) {
      pre[1] = Math.max(pre[1], cur[1]);
    } else {
      res.push(pre);
      pre = cur;
    }
  }
  res.push(pre);
  return res;
};

# 会议室 1

// 思路：判断领导是否能全部参加完成 也就是说比较当前的会议时间是否在set集合中，在的话就说明有重叠，返回false

const arr = [
  [8, 9],
  [9, 10],
  [9, 12],
  [14, 16],
  [15, 16]
];
function f(arr) {
  let set = new Set();
  for (let i = 0; i < arr.length; i++) {
    for (let j = arr[i][0]; j < arr[i][1]; j++) {
      if (set.has(j)) {
        return false;
      } else {
        set.add(j);
      }
    }
  }
  return true;
}
console.log(f(arr));

# 会议室 2

const arr = [
  [8, 9],
  [9, 10],
  [9, 12],
  [14, 16],
  [15, 16]
];
function f(arr) {
  let start = arr.map(item => item[0]);
  let end = arr.map(item => item[1]);
  start.sort((a, b) => a - b);
  end.sort((a, b) => a - b);
  let count = 0;
  let endIndex = 0;
  for (let s of start) {
    if (s >= end[endIndex]) {
      endIndex++;
    } else {
      count++;
    }
  }
  return count;
}
console.log(f(arr));

# 用最少数量的箭引爆气球 (opens new window)

/**
 * 思路： 乍一看，题目没读懂，仔细读之后发现这道题就是求重叠的区间的数量，和上面的区间重叠问题只有一个不同点，那就是如果Start = end 也会重叠
 *
 * 这里求的是不重叠区间的个数
 *
 */
var findMinArrowShots = function(points) {
  if (!points.length) {
    return 0;
  }
  points = points.sort((a, b) => a[1] - b[1]);
  let count = 1;
  let end_x = points[0][1];
  for (const point of points) {
    let start = point[0];
    if (start > end_x) {
      count++;
      end_x = point[1];
    }
  }
  return count;
};

# 剪绳子 (opens new window)

var cuttingRope = function(n) {
  /**
   * 8 = 3 + 3 + 2
   * 根据贪心算法应该讲n分成多个3，但是有一种特殊情况，那就是n % 3 === 1，其实就是结尾是3和1，那么这两个数应该换成两个2，乘积会更大
   * 
   * 所以有以下情况
   * n 除以 3 的结果为 a，余数为 b；
    当 b 为 0 时，直接将 a 个 3 相乘；
    当 b 为 1 时，将 (a - 1) 个 3 相乘，再乘以 4；
    当 b 为 2 时，将 a 个 3 相乘，再乘以 2
   */
  if (n === 2) {
    return 1;
  }
  if (n === 3) {
    return 2;
  }
  // a
  const a = Math.floor(n / 3);
  // 余数b
  const b = n % 3;
  if (b === 0) {
    return Math.pow(3, a);
  } else if (b === 1) {
    return Math.pow(3, a - 1) * 4;
  } else if (b === 2) {
    return Math.pow(3, a) * 2;
  }
};

# 跳跃游戏 (opens new window)

var canJump = function(nums) {
  /**
   * 元素可达的最大位置: nums[i] + i.如果每次更新的最大位置喜小于数组长度，则无法到达
   */
  let k = 0;
  for (let i = 0; i < nums.length; i++) {
    if (i > k) return false;
    k = Math.max(k, nums[i] + i);
  }
  return true;
};

# 前缀和

# 和为 K 的子数组 (opens new window)

var subarraySum = function(nums, k) {
  /**
   * 1. 暴力法 假设i到j的和为k
   *    sum(i,j) = i到j的nums[i]累加
   *
   * 2. 前缀和
   *
   * 3. 哈希表+前缀和 记录前缀和和出现的次数，当前缀和等于preSum-k时数量累加
   */

  // 暴力法 ，超时
  // let res = 0
  // if(!nums.length)return 0
  // for(let i = 0;i<nums.length;i++){
  //     // 每次去计算i到j的和即可，不需要计算(0，i-1)
  //     let sum = 0
  //     for(let j = i;j<nums.length;j++){
  //         sum+=nums[j]
  //         if(sum === k){
  //             res++
  //         }
  //     }
  // }
  // return res

  // 前缀和 超时
  //    let n = nums.length
  //   if (!n) {
  //     return 0
  //   }

  //   let sums = []
  //   sums[0] = 0
  //   for (let i = 1; i <= n; i++) {
  //     sums[i] = sums[i - 1] + nums[i - 1]
  //   }

  //   let res = 0
  //   for (let left = 0; left < n; left++) {
  //     for (let right = left; right < n; right++) {
  //       let sum = sums[right + 1] - sums[left]
  //       if (sum === k) {
  //         res += 1
  //       }
  //     }
  //   }
  //   return res

  // 前缀和加上哈希表
  const mp = new Map();
  // 前缀和0,次数为1
  mp.set(0, 1);
  let count = 0,
    pre = 0;
  for (const x of nums) {
    pre += x;
    // 前缀和等于pre-k 说明符合条件,累加次数
    if (mp.has(pre - k)) {
      count += mp.get(pre - k);
    }
    mp.set(pre, mp.has(pre) ? mp.get(pre) + 1 : 1);
  }
  return count;
};

# 字符串

# 电话号码的字母组合 (opens new window)

var letterCombinations = function(digits) {
  /**
   * 思路：回溯算法
   * 1. 路径：这里是数字代表的字母之间的组合
   * 2. 选择列表：当前选择数字代表的一组字符列表
   * 3. 结束条件：当前选择到的数字下标等于digits的长度，代表遍历完了
   */
  if (digits.length === 0) {
    return [];
  }
  let map = ["", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"];
  let res = [];
  // 代表已经确定的字母组合
  let path = [];
  // index代表选择到的数字下标
  function backTrack(digits, index) {
    if (index === digits.length) {
      // 路径需要转换成字符
      res.push(path.join(""));
      return;
    }
    // 获取当前数字的字母字符串
    let digit = digits[index];
    let letter = map[digit];
    for (let i = 0; i < letter.length; i++) {
      // 做选择
      path.push(letter[i]);
      backTrack(digits, index + 1);
      path.pop();
    }
  }
  backTrack(digits, 0);
  return res;
};

# 移动零 (opens new window)

var moveZeroes = function(nums) {
  let i = 0,
    j = 0;
  while (i < nums.length) {
    if (nums[i] != 0) {
      if (j < i) {
        nums[j] = nums[i];
        nums[i] = 0;
      }
      j++;
    }
    i++;
  }
  return nums;
};

# 回文子串个数 (opens new window)

var countSubstrings = function(s) {
  // 双循环 计算出组合字符串，然后判断
    let res = 0; //记录结果
    for(let i=0;i<s.length;i++){
        let str = ''; //正向组合字符串
        let restr = ''; //反向组合字符串
        for(let j=i;j<s.length;j++){
            str += s[j];
            restr = s[j] + restr;
            if(str == restr) res++;
        }
    }
    return res

# 删除字符串中所有相邻 ed 重复项 (opens new window)

var removeDuplicates = function(S) {
  let stock = [];
  for (let item of S) {
    if (stock[stock.length - 1] === item) {
      stock.pop();
    } else {
      stock.push(item);
    }
  }
  return stock.join("");
};

# 比较版本号 (opens new window)(高频 ❤️❤️❤️)

var compareInt = function(arr1, arr2) {
  let len = Math.max(arr1.length, arr2.length);
  while (arr1.length < len) arr1.push(0);
  while (arr2.length < len) arr2.push(0);
  for (let i = 0; i < len; i++) {
    if (arr1[i] > arr2[i]) return 1;
    else if (arr1[i] < arr2[i]) return -1;
  }
  return 0;
};
var compareVersion = function(version1, version2) {
  let v1 = version1.split(".");
  let v2 = version2.split(".");
  v1 = v1.map(item => Number.parseInt(item));
  v2 = v2.map(item => Number.parseInt(item));
  return compareInt(v1, v2);
};

# 括号生成 (opens new window)(高频 ❤️❤️❤️)

var generateParenthesis = function(n) {
  /**
   * 思路：回溯
   * 路径: 已拼接的字符
   * 选择列表：左括号和右括号
   * 结束条件：
   * 1. 左括号数量等于右括号
   * 2. 左括号 + 右括号数量 = 2 * n
   *
   * === > l === r  === n
   *
   * 剪枝：左括号数小于右括号
   */

  let res = [];
  // 左右括号数，当前拼接的字符串
  function backTrack(l, r, str) {
    if (l === n && r === n) {
      res.push(str);
      return;
    }
    // 剪枝
    if (l < r) {
      return;
    }
    // 插入左括号
    if (l < n) {
      backTrack(l + 1, r, str + "(");
    }
    // 插入右括号
    if (r < l) {
      backTrack(l, r + 1, str + ")");
    }
  }
  backTrack(0, 0, "");
  return res;
};

# 最长公共前缀 (opens new window)(高频 ❤️❤️❤️)

var longestCommonPrefix = function(strs) {
  /**
   * 思路：首先将数组排序，然后取出最短的和最长的字符进行比较，如果a[i] === b[i],str+=a[i]
   */
  if (!strs.length) {
    return "";
  }
  let str = "";
  // 排序
  strs = strs.sort();
  let a = strs[0];
  let b = strs[strs.length - 1];
  for (let i = 0; i < a.length; i++) {
    // 保证b取得到值,否则终止循环
    if (i < b.length && a[i] === b[i]) {
      str += a[i];
    } else {
      break;
    }
  }
  return str;
};

# 字符串相加 (opens new window)(高频 ❤️❤️❤️)

这道题就是大数相加

let addString = (num1, num2) => {
  // // 首先补零，然后从右往左相加(先从个位数相加)，考虑进位，如果两数之和大于9，进位置为1，否则置为0
  while (num1.length > num2.length) num2 = "0" + num2;
  while (num2.length > num1.length) num1 = "0" + num1;
  let res = "";
  let carry = 0; // 进位
  for (let i = num1.length - 1; i >= 0; i--) {
    const sum = +num1[i] + +num2[i] + carry;
    // 最后结果就是每次两数之和个位数拼接res，也就是sum%10+res
    res = (sum % 10) + res;
    carry = sum > 9 ? 1 : 0;
  }
  // 最后也需要考虑进位是否存在.存在就需要补1
  return carry === 1 ? "1" + res : res;
};

# 字符串相乘 (opens new window)(高频 ❤️❤️❤️)

https://leetcode-cn.com/problems/multiply-strings/solution/shi-pin-jiang-jie-43-zi-fu-chuan-xiang-cheng-by-hy/

// 用一个pos数组来求解答案，数组长度为len1+len2，默认值为0
// sum = n1 * n2 + pos[i+j+1]
// 需要做的事情就是更新 pos[i+j+1],每次pos[i+j+1] = sum % 10，然后pos[i+j] = sum / 10 | 0
// 最后处理一下前面0的情况 while循环
var multiply = function(num1, num2) {
  let len1 = num1.length;
  let len2 = num2.length;
  let pos = Array(len1 + len2).fill(0);

  for (let i = len1 - 1; i >= 0; i--) {
    let n1 = +num1[i];
    for (let j = len2 - 1; j >= 0; j--) {
      let n2 = +num2[j];
      let multi = n1 * n2;
      let sum = pos[i + j + 1] + multi;

      pos[i + j + 1] = sum % 10;
      pos[i + j] += (sum / 10) | 0;
    }
  }
  // 去除前置的‘0’的情况
  while (pos[0] == 0) {
    pos.shift();
  }
  return pos.length ? pos.join("") : "0";
};

# 翻转字符串里的单词 (opens new window)(高频 ❤️❤️❤️)

// 思路：去重两边空白字符然后转为数组反转，接着转为字符串
var reverseWords = s => {
  return s
    .trim()
    .split(/\s+/)
    .reverse()
    .join(" ");
};

变形版

/**
 * @param {string} s
 * @return {string}
 */
var reverseWords = function(s) {
  let arr = s.split(" ");
  let res = arr.map(item => {
    return item
      .split("")
      .reverse()
      .join("");
  });
  return res.join(" ");
};

# 排序和搜索(高频 ❤️❤️❤️)

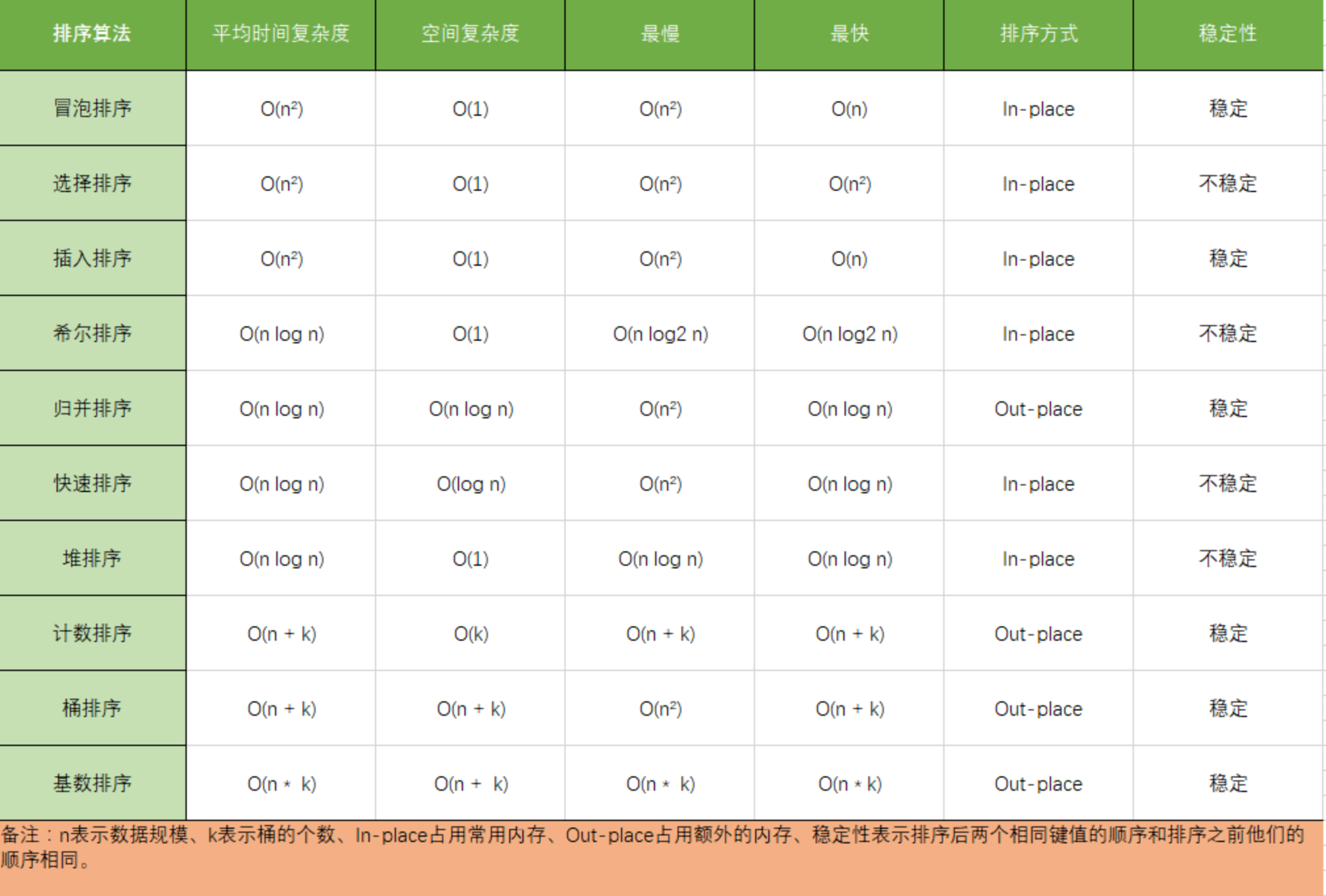
# 冒泡排序

Array.prototype.bunbleSort = function() {
  for (let i = 0; i < this.length - 1; i++) {
    for (let j = 0; j < this.length - 1 - i; j++) {
      if (this[j] > this[j + 1]) {
        const temp = this[j];
        this[j] = this[j + 1];
        this[j + 1] = temp;
      }
    }
  }
};

# 插入排序

//插入: 从第二个数开始往前比 如果前面某个数比第二个数要大，就将这个数往后排，如果不大就停止，最后获取到的j就是要插入的位置
function insertSort(arr) {
  for (let i = 1; i < arr.length; i++) {
    let temp = arr[i];
    let j = i;
    while (j > 0) {
      // 判断前面的数是否大于temp，大的话就交换j和j-1的位置
      if (arr[j - 1] > temp) {
        arr[j] = arr[j - 1];
      } else {
        break;
      }
      j--;
    }
    // 插入的位置就是j
    arr[j] = temp;
  }
  return arr;
}
console.log(insertSort([212, 12, 12, 31, 1, 34, 2, 5]));

# 归并排序

// 归并 先分成子有序数组 最后合并为大数组，合并有效数组就是比较对头，将较小者对头推入新数组中即可
Array.prototype.mergeSort = function() {
  const rec = arr => {
    if (arr.length <= 1) {
      return arr;
    }
    const mid = Math.floor(arr.length / 2);
    const left = arr.slice(0, mid);
    // 注意这里是arr.length 而不是-1
    const right = arr.slice(mid, arr.length);
    // 递归 这里其实就是在将分好的左右数组再劈成两半
    const orderLeft = rec(left);
    const orderRight = rec(right);

    // 接下来合并数组，合并数组就是分别取出对头进行比较
    const res = [];
    while (orderLeft.length || orderRight.length) {
      if (orderLeft.length && orderRight.length) {
        res.push(orderLeft[0] < orderRight[0] ? orderLeft.shift() : orderRight.shift());
      } else if (orderLeft.length) {
        res.push(orderLeft.shift());
      } else if (orderRight.length) {
        res.push(orderRight.shift());
      }
    }
    return res;
  };
  const result = rec(this);
  result.forEach((n, i) => {
    this[i] = n;
  });
};

# 快速排序(高频 ❤️❤️❤️)

// 快速: 选择基准 ，将数组拆分左右数组，直到array的长度小于等于1递归结束

Array.prototype.quickSort = function() {
  const rec = arr => {
    if (arr.length <= 1) {
      return arr;
    }
    const left = [];
    const right = [];
    const mid = arr[0];
    for (let i = 1; i < arr.length; i++) {
      if (arr[i] < mid) {
        left.push(arr[i]);
      } else {
        right.push(arr[i]);
      }
    }
    return [...rec(left), mid, ...rec(right)];
  };
  const result = rec(this);
  result.forEach((n, i) => {
    this[i] = n;
  });
};

# 选择排序

// 选择 : 计算出[i,arr.length-1]的最小值，还有下标，然后和当前遍历到的元素交换位置

function selectSort(arr) {
  for (let i = 0; i < arr.length; i++) {
    let min = Math.min(...arr.slice(i));
    let index = arr.indexOf(min);
    [arr[i], arr[index]] = [arr[index], arr[i]];
  }
  return arr;
}
console.log(selectSort([21, 1, 2, 6, 1, 3]));

# 堆排序

/**
 * 思路： 堆排序需要三个方法：主体函数 + 构建堆 + 调整堆
 */

// 主方法: 首先构建堆，遍历数组，这个时候第一个元素就是最大值，将堆头和尾元素更换位置，length-1，继续调整堆调换位置

function heapsort(arr) {
  buildHeap(arr);
  for (let i = arr.length - 1; i > 0; i--) {
    // 交换
    swap(arr, 0, i);
    // 下移调整
    heapify(arr, 0, i);
  }
  return arr;
}
function buildHeap(arr) {
  if (!arr.length) {
    return;
  }
  // 只有Math.floor(len/2-1)需要调整，记得此处i可以等于0
  for (let i = Math.floor(arr.length / 2 - 1); i >= 0; i--) {
    heapify(arr, i, arr.length);
  }
}

// 堆调整：找到子节点最大的，然后交换父子节点，循环结束要重新赋值父节点，表示找到了位置,可以理解为下移操作
function heapify(arr, parent, length) {
  let temp = arr[parent];
  let childIndex = 2 * parent + 1;
  // 找到最大节点下标
  while (childIndex < length) {
    if (childIndex + 1 < length && arr[childIndex + 1] > arr[childIndex]) {
      childIndex++;
    }
    // 不符合大顶堆则跳出循环
    if (arr[childIndex] <= arr[parent]) {
      break;
    }
    arr[parent] = arr[childIndex];
    parent = childIndex;
    childIndex = 2 * parent + 1;
  }
  //循环结束要重新赋值父节点
  arr[parent] = temp;
}

function swap(arr, i, j) {
  let temp = arr[i];
  arr[i] = arr[j];
  arr[j] = temp;
}
let arr1 = [1, 21, 12312312, 3312, 234, -1];
console.log(heapsort(arr1));

# 各排序算法的稳定性，时间复杂度，空间复杂度 (opens new window)

# 二分法和进阶

首先常规的二分查找不用多说直接上

function binarySearch(arr, item) {
  let low = 0;
  let high = arr.length - 1;
  while (low <= high) {
    let mid = Math.floor((low + high) / 2);
    let Element = arr[mid];
    if (Element === item) {
      return mid;
    } else if (Element > item) {
      high = mid - 1;
    } else if (Element < item) {
      low = mid + 1;
    }
  }
  return -1;
}

但是这个常规的二分查找无法处理一下情形

输入 [1,2,3,3,4] ,3

这个时候我们在搜索的如果中间位元素等于搜索元素就不能直接返回，要分两种情况了。一句话就是，寻找数组左侧第一位，就要缩小右侧边界范围，寻找右侧第一位，就要缩小左侧边界范围,然后检查数组越界也需要格外注意

左侧边界查找：[left,right), 当**nums[mid] == target**时不要立即返回而要收紧右侧边界(**high = mid -1**)以锁定左侧边界

function leftBoundSearch(arr, item) {
  let low = 0;
  let high = arr.length - 1;
  while (low <= high) {
    // 切记 取值一定要定义在里面，不然会报错
    let mid = Math.floor((low + high) / 2);
    let Element = arr[mid];
    if (Element === item) {
      high = mid - 1;
    } else if (Element > item) {
      high = mid - 1;
    } else if (Element < item) {
      low = mid + 1;
    }
  }
  // 检查数组越界
  if (low >= arr.length || arr[left] !== item) {
    return -1;
  }
  return left;
}

右侧边界查找：(left,right],当**nums[mid] == target**时不要立即返回而要收紧左侧边界(**low = mid +1**)以锁定右侧边界

function rightBoundSearch(arr, item) {
  let low = 0;
  let high = arr.length - 1;
  while (low <= high) {
    let mid = Math.floor((low + high) / 2);
    let Element = arr[mid];
    if (Element === item) {
      low = mid + 1;
    } else if (Element > item) {
      high = mid - 1;
    } else if (Element < item) {
      low = mid + 1;
    }
  }
  // 检查数组越界
  if (high < 0 || arr[right] !== item) {
    return -1;
  }
  return right;
}

# 矩阵

# 矩阵查找 (opens new window)(高频 ❤️❤️❤️)

/**
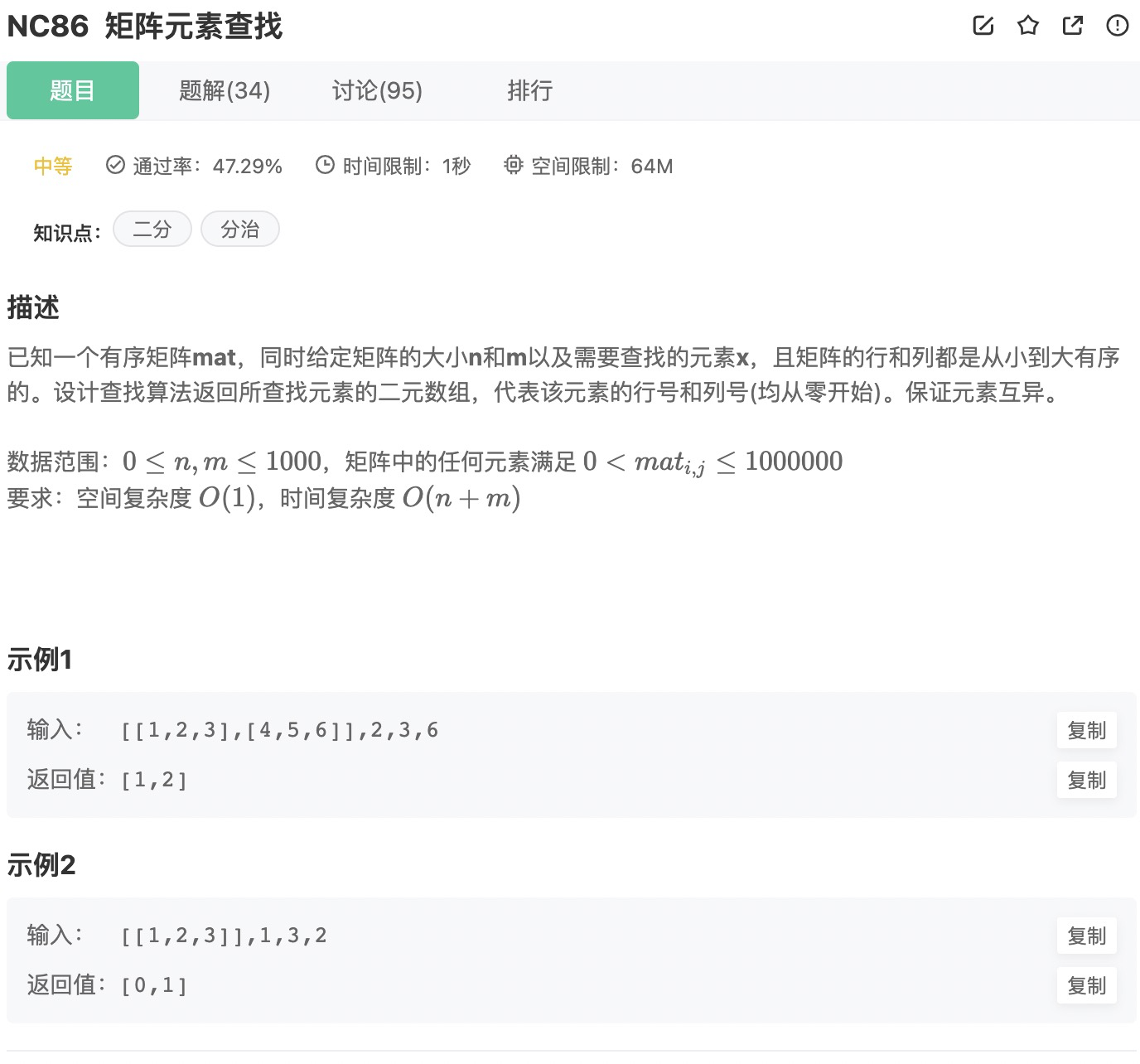
 * 思路：这里就是利用两个指针，分别代表行和列，因为是有序矩阵，如果查找的元素比当前元素小，则扩大，也就是行++，反之列--
 * */

function findElement(mat, n, m, x) {
  // 行数等于二维矩阵的数组大小,矩阵第一个元素数组大小等于列数
  if (!mat.length || mat.length !== n || mat[0].length !== m) {
    return [];
  }
  let row = 0;
  let col = mat[0].length - 1;
  while (row <= mat.length - 1 && col >= 0) {
    if (mat[row][col] === x) {
      return [row, col];
    } else if (mat[row][col] > x) {
      col--;
    } else {
      row++;
    }
  }
  return [];
}

# 搜索二维矩阵 II (opens new window)(高频 ❤️❤️❤️)

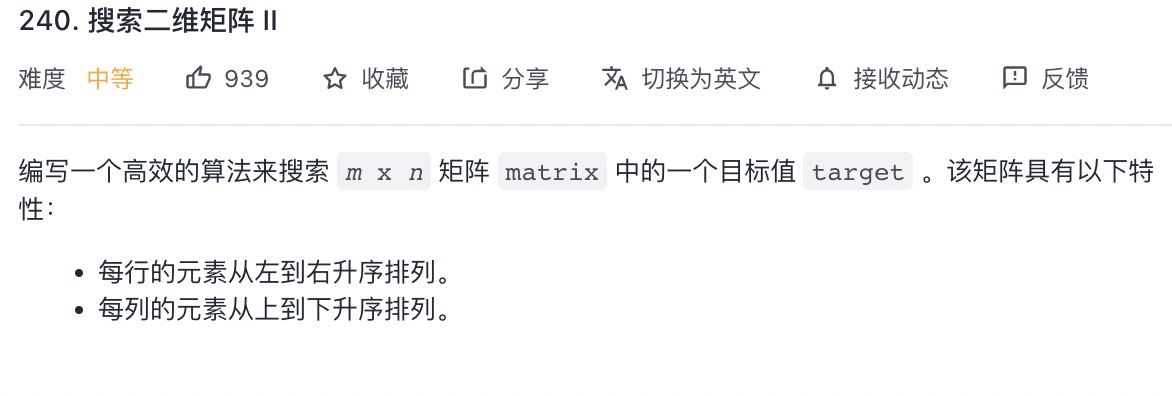
var searchMatrix = function(matrix, target) {
  if (!matrix.length) return false;
  let row = 0;
  let col = matrix[0].length - 1;
  while (row <= matrix.length - 1 && col >= 0) {
    if (matrix[row][col] === target) {
      return true;
    } else if (matrix[row][col] < target) {
      row++;
    } else {
      col--;
    }
  }
  return false;
};

# 顺时针打印矩阵 (opens new window)(高频 ❤️❤️❤️)

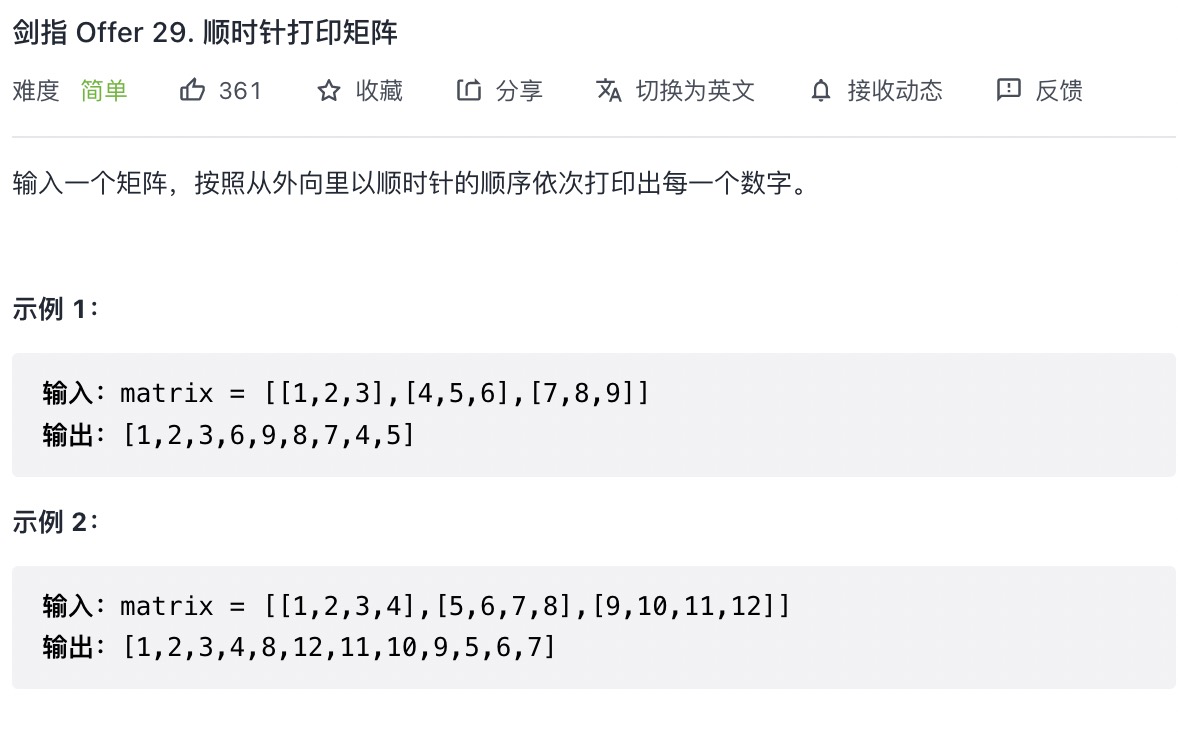
var spiralOrder = function(matrix) {
  // 一层一层的剥开 首先第一层数组，然后最右层数组 然后最下层数组，然后最下层数组
  const res = [];
  while (matrix.length) {
    let topArray = matrix.shift();
    let rightArray = matrix.map(item => item.pop());
    let bottomArray = matrix.pop();
    let leftArray = matrix.map(item => item.shift());

    topArray && res.push(...topArray);
    rightArray && res.push(...rightArray);
    bottomArray && res.push(...bottomArray.reverse());
    leftArray && res.push(...leftArray.reverse());
  }
  return res.filter(item => item !== undefined);
};

# 矩阵旋转 180deg(螺旋矩阵 (opens new window))(高频 ❤️❤️❤️)

function fn(array) {
  let dd = [];
  dd = array.map((val, index) => {
    let arr = [];
    for (let i = val.length - 1; i >= 0; i--) {
      arr.push(array[i][index]);
    }
    return arr;
  });
  return dd;
}

# 对角线遍历 (opens new window)(高频 ❤️❤️❤️)

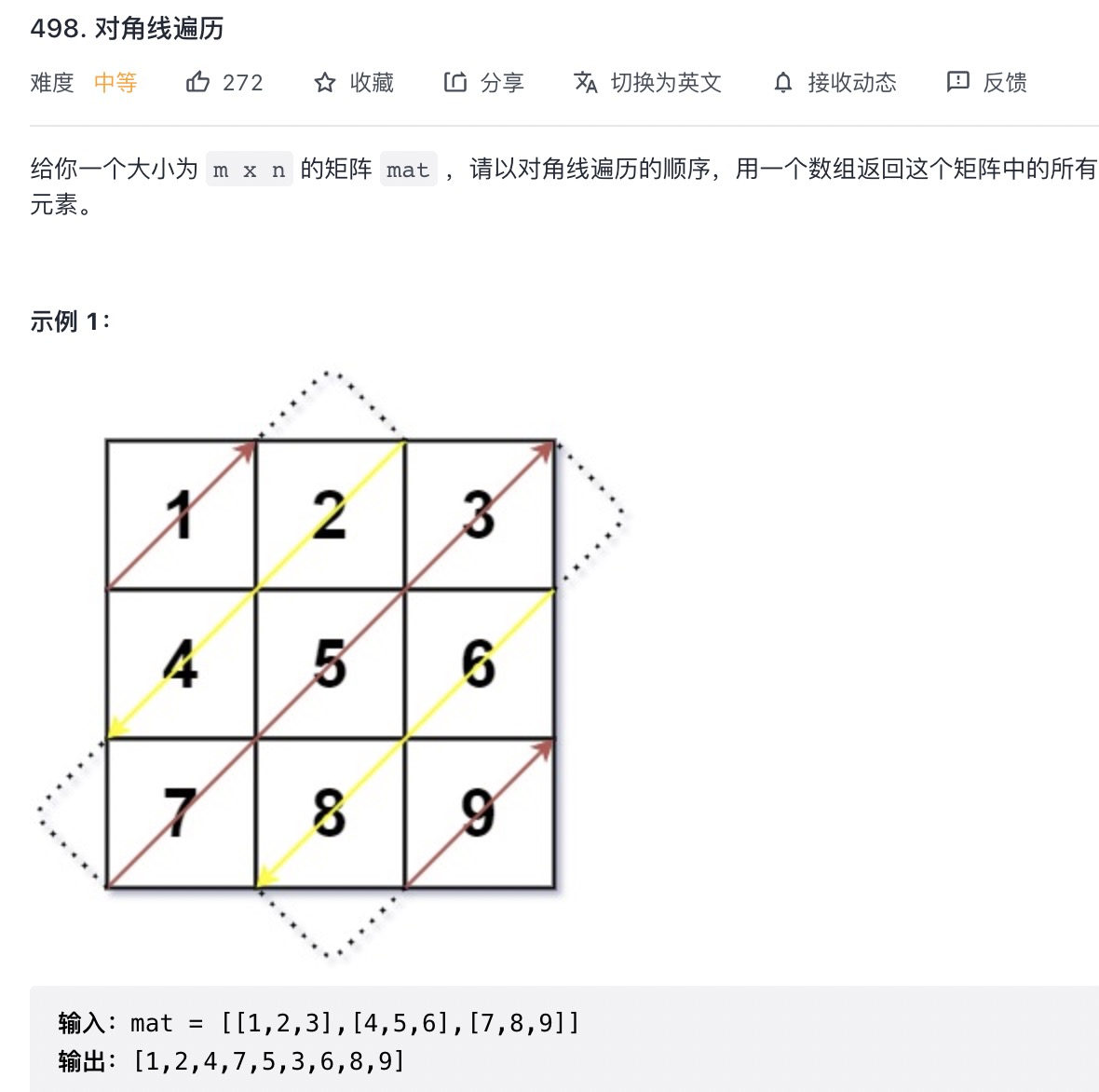
var findDiagonalOrder = function(matrix) {
  if (!matrix.length) return []; //处理空数组
  let n = matrix.length; //n行
  let m = matrix[0].length; //m列
  let level = m + n - 1; //n+m-1等于以对角线方式遍历的层数，层数以索引为0开始
  let res = [matrix[0][0]]; //直接把第一个元素放进去

  for (let index = 1; index < level; index++) {
    //我们对以对角线方式的每一层进行遍历
    if (index % 2 == 0) {
      //当层数的索引为偶数时候，向上遍历，对角线上元素的横坐标从最大层索引递减
      for (let row = index; row >= 0; row--) {
        let col = index - row;
        if (row < n && col < m) {
          res.push(matrix[row][col]);
        }
      }
    } else {
      //当层数的索引为奇数时候，向下遍历，对角线上元素的纵坐标从最大层索引递减
      for (let col = index; col >= 0; col--) {
        let row = index - col;
        if (row < n && col < m) {
          res.push(matrix[row][col]);
        }
      }
    }
  }
  return res;
};

# 旋转图像 (opens new window)(高频 ❤️❤️❤️)

var rotate = function(matrix) {
  // 转置，然后再水平对折
  const m = matrix.length;
  for (let i = 0; i < m; i++) {
    for (let j = i; j < m; j++) {
      [matrix[i][j], matrix[j][i]] = [matrix[j][i], matrix[i][j]];
    }
  }
  matrix = matrix.map(item => item.reverse());
};

# 矩阵置零 (opens new window)

//利用了js的特性，-0和0的不相等
//将0所在行列中非0元素置为-0
var setZeroes = function(matrix) {
  for (let i = 0; i < matrix.length; i++) {
    for (let j = 0; j < matrix[i].length; j++) {
      if (Object.is(matrix[i][j], 0)) {
        for (let k = 0; k < matrix.length; k++) {
          if (k !== i && Object.is(matrix[k][j], 0)) continue;
          else matrix[k][j] = -0;
        }
        for (let k = 0; k < matrix[i].length; k++) {
          if (k !== j && Object.is(matrix[i][k], 0)) continue;
          else matrix[i][k] = -0;
        }
      }
    }
  }
  return matrix;
};

# 智力题

题集 (opens new window)

题库 2 (opens new window)

约瑟夫环问题

var lastRemaining = function(n, m) {
  /* 
        约瑟夫环 正向递归 ｜逆向迭代 
        因为是从数字0开始 故 索引和数组值是一直的 nums[i] = i
        1. 逆向思维 遍历迭代 最后肯定是只剩下一个人 且 此时的索引为0 故从倒数第二轮反推
        2. 正向递归 终止条件为 n = 1 即数组中只剩下一个人返回此时索引 0
        (当前index + m) % 上一轮剩余数字的个数
        关键代码：当前轮最后剩下的数字 = (上一轮剩下的数字索引 + 计数的距离m) %（模上）当前数组/圆圈长度l
        推到公式
        fn(n, m) = n === 1 ? 0 : (fn(n - 1, m) + m)  % n
        i为最终轮时 幸存数所在数组内的索引
    */
  let i = 0;

  for (let l = 2; l <= n; l++) i = (i + m) % l;

  return i;

  // 2. 递归实现 当数组中长度大于等于2时 继续递归下去 直到n = 1
  return n > 0 ? (lastRemaining(n - 1, m) + m) % n : 0;
};

# 单调栈

# 单调栈数组

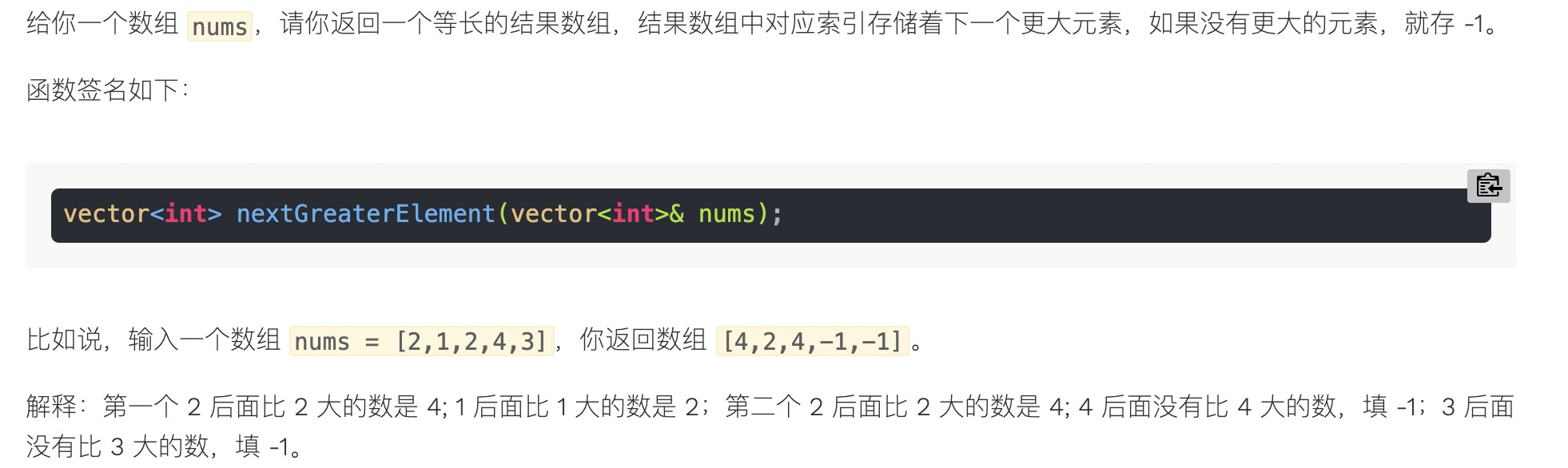
function nextGreaterElement(nums: nums[]) {
  let res = [];
  let stack = [];
  for (let i = nums.length - 1; i >= 0; i--) {
    while (stack.length && stack[stack.length - 1] <= nums[i]) {
      stack.pop();
    }
    res[i] = stack.length ? stack[stack.length - 1] : 0;
    stack.push(nums[i]);
  }
}

# 每日温度 (opens new window)

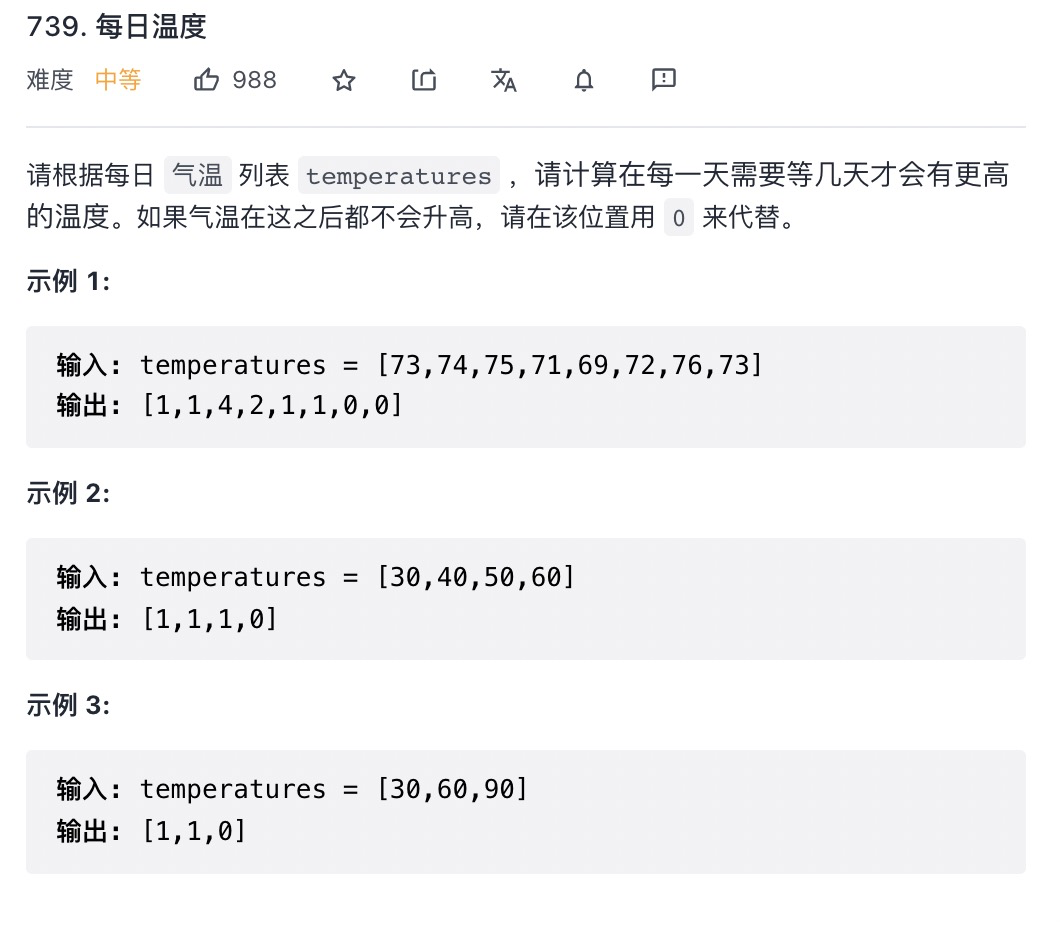
var dailyTemperatures = function(temperatures) {
  let stack = [];
  let res = [];
  for (let i = temperatures.length - 1; i >= 0; i--) {
    // 判断栈顶下的温度是否小于等于当前遍历温度
    while (stack.length && temperatures[stack[stack.length - 1]] <= temperatures[i]) {
      stack.pop();
    }
    // 栈顶元素 - i 即刚超过距离
    res[i] = stack.length ? stack[stack.length - 1] - i : 0;
    stack.push(i);
  }
  return res;
};

# 其他类型

# 找到所有数组中消失的数字 (opens new window)

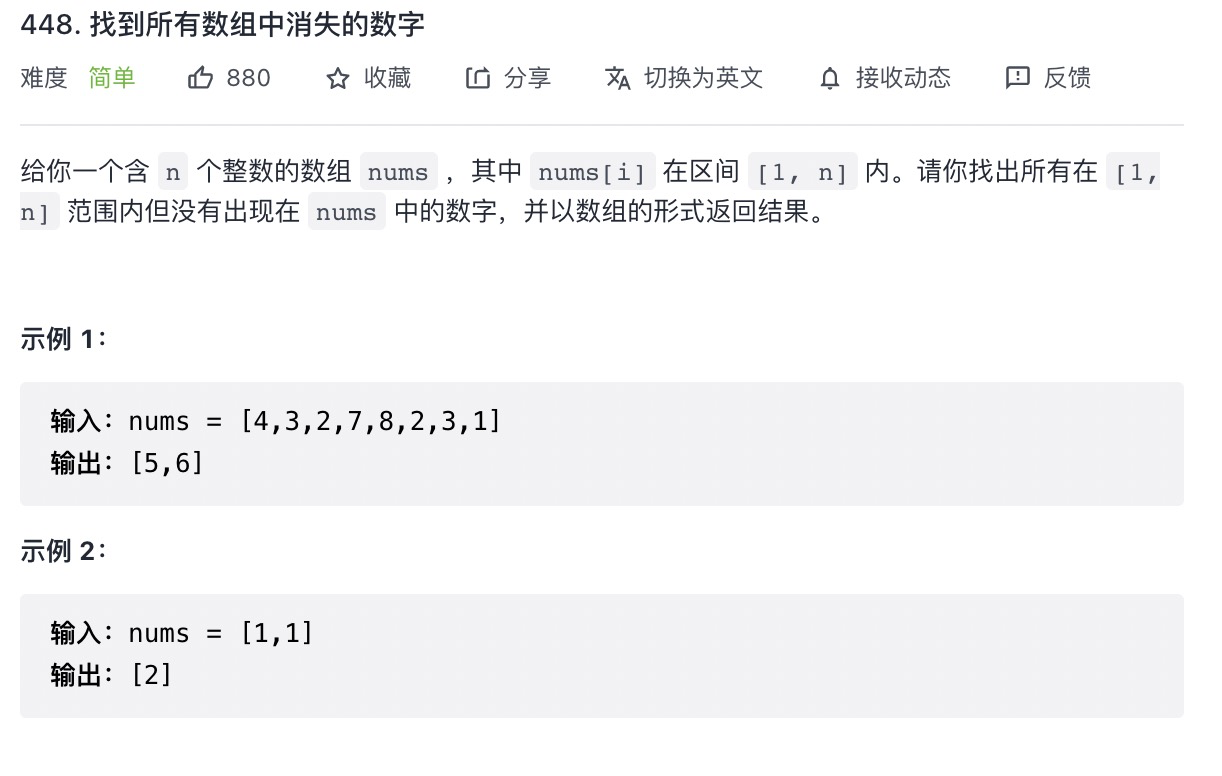
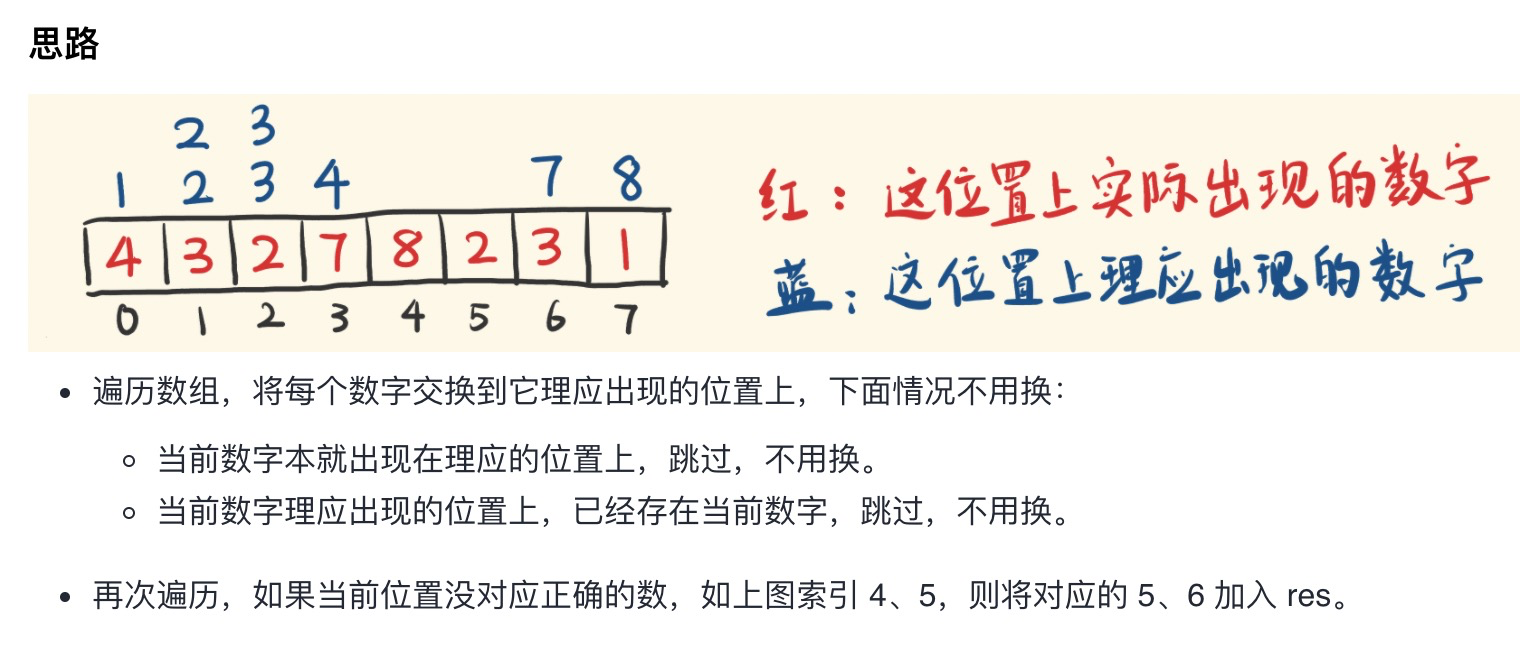
var findDisappearedNumbers = function(nums) {
  let res = [];
  let i = 0;
  while (i < nums.length) {
    // 理应出现位置命中,跳过本次循环
    if (nums[i] === i + 1) {
      i++;
      continue;
    }
    // 理应出现数字和实际有重复
    const ideaIndex = nums[i] - 1;
    if (nums[i] === nums[ideaIndex]) {
      i++;
      continue;
    }
    // 交换数字，替换成理应出现数字
    [nums[i], nums[ideaIndex]] = [nums[ideaIndex], nums[i]];
  }

  for (let i = 0; i < nums.length; i++) {
    if (nums[i] !== i + 1) {
      res.push(i + 1);
    }
  }

  return res;
};

# 寻找两个正序数组的中位数 (opens new window)(高频 ❤️❤️❤️)

/**
 * @param {number[]} nums1
 * @param {number[]} nums2
 * @return {number}
 */
var findMedianSortedArrays = function(nums1, nums2) {
  // 排序之后计算中位数
  const arr = [...nums1, ...nums2].sort((a, b) => a - b);
  return (arr[Math.floor((arr.length - 1) / 2)] + arr[Math.floor(arr.length / 2)]) / 2;
};

# 只出现一次的数字 (opens new window)

var singleNumber = function(nums) {
  let map = new Map();
  for (let c of nums) {
    map.set(c, map.has(c) ? map.get(c) + 1 : 1);
  }
  for (let [key, value] of map) {
    if (value === 1) {
      return key;
    }
  }
};

# 字母异位词分组 (opens new window)

/**
 * @param {string[]} strs
 * @return {string[][]}
 */
var groupAnagrams = function(strs) {
  // 先拿到排序后字符串数组
  let temp = strs.map(item => {
    return item
      .split("")
      .sort((a, b) => a.charCodeAt() - b.charCodeAt())
      .join("");
  });
  // 用map保存，key为temp[i],value为[str[i]]
  // 如果没有遇到重复的value，map.set(temp[i],[strs[i]])
  // 遇到重复的,往这个value数组添加strs[i]
  let map = new Map();
  for (let i = 0; i < temp.length; i++) {
    if (map.get(temp[i])) {
      map.get(temp[i]).push(strs[i]);
    } else {
      map.set(temp[i], [strs[i]]);
    }
  }
  return Array.from(map.values());
};

# 连续数组 (opens new window)

var findMaxLength = function(nums) {
  const n = nums.length;
  const map = new Map();
  map.set(0, -1);
  // 前缀和
  let pre = 0;
  let res = 0;
  for (let i = 0; i < n; i++) {
    pre += nums[i] == 0 ? -1 : 1;
    // 如果存在的话，则将当前索引和之前存入的索引值相减  取题目要求的最大值
    if (map.has(pre)) {
      res = Math.max(res, i - map.get(pre));
    } else {
      // 记录前缀和索引
      map.set(pre, i);
    }
  }
  return res;
};

# LRU 缓存 (opens new window)(高频 ❤️❤️❤️)

/**
 * @param {number} capacity
 */
var LRUCache = function(capacity) {
  this.capacity = capacity;
  this.map = new Map();
};

/**
 * @param {number} key
 * @return {number}
 */
LRUCache.prototype.get = function(key) {
  if (this.map.has(key)) {
    let temp = this.map.get(key);
    this.map.delete(key);
    this.map.set(key, temp);
    return temp;
  } else {
    return -1;
  }
};

/**
 * @param {number} key
 * @param {number} value
 * @return {void}
 */
LRUCache.prototype.put = function(key, value) {
  if (this.map.has(key)) {
    this.map.delete(key);
  }
  this.map.set(key, value);
  if (this.map.size > this.capacity) {
    this.map.delete(this.map.keys().next().value);
  }
};

/**
 * Your LRUCache object will be instantiated and called as such:
 * var obj = new LRUCache(capacity)
 * var param_1 = obj.get(key)
 * obj.put(key,value)
 */

← 算法解题模板剑指Offer →